2.3 行列のいろいろ 〜 零行列,正方行列,対角行列,単位行列
定義 2.10 (零行列)
成分が全て零の行列
を零行列(zero matrix)と呼ぶ.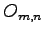 は
は 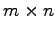 型の零行列を意味する.
型の零行列を意味する.
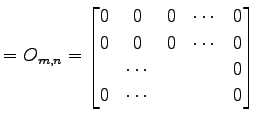 |
(262) |
を零行列(zero matrix)と呼ぶ.
定義 2.11 (正方行列)
行と列の数が等しい行列
を正方行列(square matrix)と呼ぶ. 行列の成分のうち左上から右下へ並んでいる成分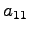 ,
,
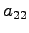 ,
,  ,
, 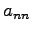 を
対角成分(diagonal components)と呼ぶ.
を
対角成分(diagonal components)と呼ぶ.
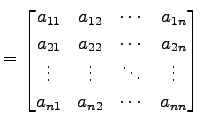 |
(263) |
を正方行列(square matrix)と呼ぶ. 行列の成分のうち左上から右下へ並んでいる成分
定義 2.12 (対角行列)
対角成分以外の成分が全て零の正方行列
を対角行列(diagonal matrix)と呼ぶ.
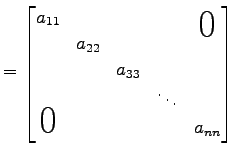 |
(264) |
を対角行列(diagonal matrix)と呼ぶ.
定義 2.13 (単位行列)
対角成分がすべて 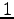 の対角行列
の対角行列
を単位行列(unit matrix)と呼ぶ.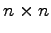 の単位行列を
の単位行列を 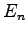 と書き
と書き 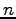 次の単位行列と呼ぶ.
単位行列は後述するように行列の積において ``
次の単位行列と呼ぶ.
単位行列は後述するように行列の積において ``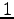 '' の役割をはたす.
'' の役割をはたす.
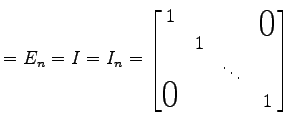 |
(265) |
を単位行列(unit matrix)と呼ぶ.
平成20年2月2日