2.2 行ベクトル,列ベクトル
定義 2.2 (行ベクトル)
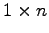 行列
行列
を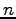 次の行ベクトル(row vector)と呼ぶ.
次の行ベクトル(row vector)と呼ぶ.
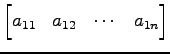 |
(254) |
を
例 2.3 (行ベクトルの具体例)
4 次の行ベクトル:
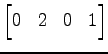 |
(255) |
定義 2.4 (列ベクトル)
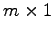 行列
行列
を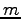 次の列ベクトル(column vector)と呼ぶ.
次の列ベクトル(column vector)と呼ぶ.
 |
(256) |
を
例 2.5 (列ベクトルの具体例)
3 次の列ベクトル:
| (257) |
注意 2.6 (ベクトルの呼び方と書き方)
行ベクトル,列ベクトルを総称してベクトル(vector)と呼ぶ.
ベクトルを表わす変数は太文字で書き,
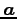 ,
, 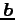 ,
, 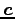 ,
, 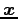 ,
, 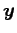 のように
表記する.
のように
表記する.
定義 2.7 (零ベクトル)
成分が全て 0 のベクトルを零ベクトルと呼び 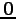 と表わす.
と表わす.
注意 2.8 (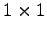 行列)
行列)
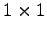 行列である
行列である ![$ [a_{11}]$](img1038.png) は要素は一つしかないが,
あくまでも行列であるので注意する.
しかしまれに数として取り扱うこともあるので,
更に注意が必要である.
は要素は一つしかないが,
あくまでも行列であるので注意する.
しかしまれに数として取り扱うこともあるので,
更に注意が必要である.
例 2.9 (行列の名称等)
行列
を考える.
(1) 行列 の型は
の型は 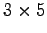 型である.
型である.
(2)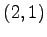 成分は
成分は 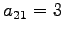 であり,
であり,
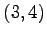 成分は
成分は 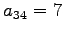 である.
である.
(3) 第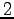 行は
行は
であり,第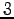 列は
列は
である.
(4) 行列 の転置行列
の転置行列 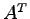 は
は
である.
 |
(258) |
を考える.
(1) 行列
(2)
(3) 第
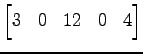 |
(259) |
であり,第
| (260) |
である.
(4) 行列
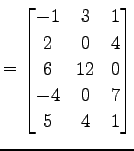 |
(261) |
である.
平成20年2月2日