3.7 行列の階数
定義 3.27 (行列の階数)
行列  を簡約化した行列を
を簡約化した行列を 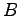 とする.
このとき
行列
とする.
このとき
行列  に対する行列の階数(rank)を
に対する行列の階数(rank)を
と定義する.
| (439) |
と定義する.
例 3.28 (階数の具体例)
 |
(440) |
定理 3.30 (階数に関する定理)
行列  が
が 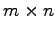 型のとき,
型のとき,
が成り立つ.
| (443) |
が成り立つ.
問 3.31
これを示せ.
問 3.32
教科書(p.27)問題2.2.
平成20年2月2日
![[*]](crossref.png)