3.11 同次形の解
定義 3.38 (同次形方程式)
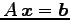 において
において 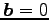 が成り立つとき,
方程式
が成り立つとき,
方程式
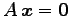 は同次形(homogeneous)と呼ぶ.
は同次形(homogeneous)と呼ぶ.
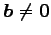 とき非同次形(inhomogeneous)と呼ぶ.
とき非同次形(inhomogeneous)と呼ぶ.
定理 3.39 (同次形の解の存在)
同次方程式は
![$ \mathrm{rank}\,(A)=\mathrm{rank}\,[A\vert\vec{0}]$](img1560.png) が常になり立つので,
常に解
が常になり立つので,
常に解
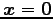 をもつ.
をもつ.
定義 3.40 (同次形の自明解)
同次方程式
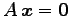 の解
の解
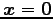 を
自明な解と呼ぶ.
を
自明な解と呼ぶ.
定理 3.41 (同次方程式の解)
同次方程式
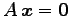 について次の条件が成り立つ:
について次の条件が成り立つ:
である. 拡大係数行列の一番右の列の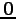 はランクに影響を与えない.
よって定理の条件を得る.
はランクに影響を与えない.
よって定理の条件を得る.
を得る.(1)の定理より自明でない解をもつ. 証明終了.
- (1)
- 自明な解
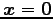 のみをもつための必用十分条件は
のみをもつための必用十分条件は
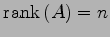
(466)
である. - (2)
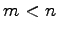 のとき,方程式は自明でない解(任意定数を含む解)をもつ.
のとき,方程式は自明でない解(任意定数を含む解)をもつ.
(証明)(1)前述の定理より唯一つの解をもつための必要十分条件は
| (467) |
である. 拡大係数行列の一番右の列の
(2)
![]() ,
,
![]() と条件
と条件 ![]() より
より
| (468) |
を得る.(1)の定理より自明でない解をもつ. 証明終了.
例 3.42 (同次形方程式の解)
方程式
を考える. 係数行列を簡約化して
を得る.よって解は
となる. 解は原点を通る2次元平面である.
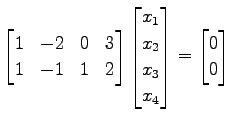 |
(469) |
を考える. 係数行列を簡約化して
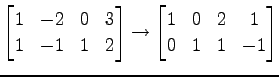 |
(470) |
を得る.よって解は
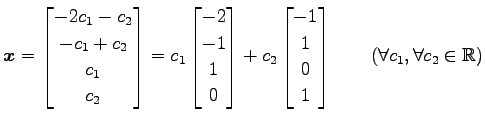 |
(471) |
となる. 解は原点を通る2次元平面である.
例 3.43 (同次形方程式の解)
方程式
を考える. 係数行列を簡約化して
を得る.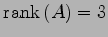 であり,
任意定数の個数は
であり,
任意定数の個数は
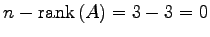 となるから,
解は一意な解となる.
以上より解は自明な解
となるから,
解は一意な解となる.
以上より解は自明な解
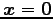 のみである.
のみである.
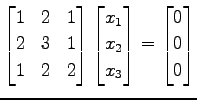 |
(472) |
を考える. 係数行列を簡約化して
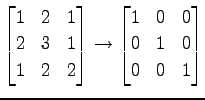 |
(473) |
を得る.
例 3.44 (同次形方程式の解)
方程式
を考える. 行の個数と列の個数をみると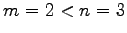 であるから,
必ず
であるから,
必ず
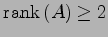 となり,
任意定数の個数は
となり,
任意定数の個数は
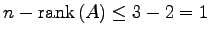 となる.
必ず
となる.
必ず 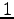 個以上の任意定数を含むから,
解は非自明な解となる.
個以上の任意定数を含むから,
解は非自明な解となる.
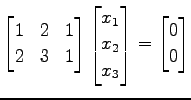 |
(474) |
を考える. 行の個数と列の個数をみると
平成20年2月2日