4.1 行列式の導出
連立 1 次方程式
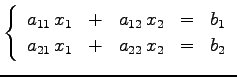 |
(565) |
を考える. このときこの方程式が一意な解ともつ条件を求める. 方程式を書き直すと
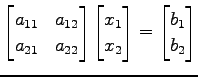 |
(566) |
となる. 拡大係数行列は
![$\displaystyle = \left[ \begin{array}{cc\vert c} a_{11} & a_{12} & b_{1} \\ a_{21} & a_{22} & b_{2} \end{array} \right]$](img1880.png) |
(567) |
である. 簡約化を行う:
![$\displaystyle \left[ \begin{array}{cc\vert c} a_{11} & a_{12} & b_{1} \\ a_{21} & a_{22} & b_{2} \end{array} \right]$](img1881.png) |
(568) | |
| (第一行に
|
(569) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{cc\vert c} a_{11} & a_{12} &...
...}}} & \displaystyle{\frac{a_{11}b_{2}-b_{1}a_{21}}{a_{11}}} \end{array} \right]$](img1883.png) |
(570) | |
| (第二行に |
(571) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{cc\vert c} a_{11} & a_{12} &...
...{22}-a_{12}a_{21}} & \displaystyle{a_{11}b_{2}-b_{1}a_{21}} \end{array} \right]$](img1884.png) |
(572) | |
| (第二行に
|
(573) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{cc\vert c} a_{11} & 0 & \dis...
...{22}-a_{12}a_{21}} & \displaystyle{a_{11}b_{2}-b_{1}a_{21}} \end{array} \right]$](img1886.png) |
(574) | |
| (第一行に |
(575) | |
| (第二行に
|
(576) | |
![$\displaystyle \longrightarrow \left[ \begin{array}{cc\vert c} 1 & 0 & \displays...
...rac{a_{11}b_{2}-b_{1}a_{21}}{a_{11}a_{22}-a_{12}a_{21}}} \end{array} \right]\,.$](img1889.png) |
(577) |
ここで
| (578) |
を条件としてかした. このとき拡大係数行列の階数は
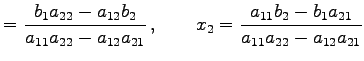 |
(579) |
をもつ. この結果より,行列
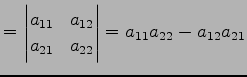 |
(580) |
と定義する.
同様にして正方行列 ![]() に対して行列式を定義すると
に対して行列式を定義すると
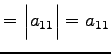 |
(581) | |
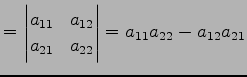 |
(582) | |
 |
(583) | |
| (584) | ||
| (585) |
となる. 一般に
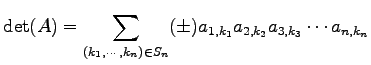 |
(586) |
となることが予想される. ここで
| (587) | ||
| (588) | ||
| (589) |
である.
平成20年2月2日