4.2 УжДЙ
ФъЕС 4.1 (ЪИЛњЄЮУжДЙ)
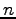 ИФЄЮЪИЛњ
ИФЄЮЪИЛњ
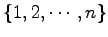 ЄЋЄщ
МЋЪЌМЋПШ
ЄЋЄщ
МЋЪЌМЋПШ
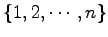 ЄиЄЮ
ЄиЄЮ
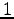 Та
Та 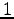 ЄЮМЬСќЄђ
ЄЮМЬСќЄђ
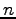 ЪИЛњЄЮУжДЙЁЪpermutationЁЫЄШЄЄЄІЁЅ
ЪИЛњЄЮУжДЙЁЪpermutationЁЫЄШЄЄЄІЁЅ
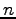 ЪИЛњЄЮУжДЙ
ЪИЛњЄЮУжДЙ 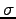 ЄЌМЬСќ
ЄЌМЬСќ
ЄЮЄШЄ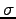 Єђ
Єђ
ЄШЩНЄяЄЙЁЅ МЬСќ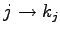 Єђ
Єђ
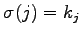 ЄШЩНЄяЄЙЁЅ
ЄШЩНЄяЄЙЁЅ
| (590) |
ЄЮЄШЄ
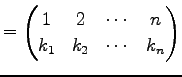 |
(591) |
ЄШЩНЄяЄЙЁЅ МЬСќ
Юу 4.2 (УжДЙЄЮЖёТЮЮу)
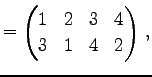 |
(592) | |
| (593) | ||
| (594) |
Юу 4.3 (УжДЙЄЮЩНЕ)
ЦБЄИПєЛњЄЫУжДЙЄЙЄыОьЙчЄЯОЪЮЌВФЧНЁЅ ЪТЄйЄыНчЄЯЄЩЄІЄЧЄтЮЩЄЄЁЅ
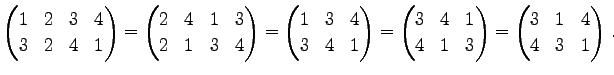 |
(595) |
ЦБЄИПєЛњЄЫУжДЙЄЙЄыОьЙчЄЯОЪЮЌВФЧНЁЅ ЪТЄйЄыНчЄЯЄЩЄІЄЧЄтЮЩЄЄЁЅ
ФъЕС 4.4 (УжДЙЄЮРб)
ЦѓЄФЄЮУжДЙ
ЄЮРб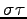 Єђ
Єђ
ЄоЄПЄЯ
ЄШФъЕСЄЙЄыЁЅ
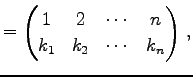 |
(596) | |
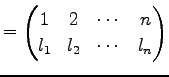 |
(597) |
ЄЮРб
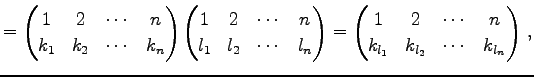 |
(598) |
ЄоЄПЄЯ
| (599) |
ЄШФъЕСЄЙЄыЁЅ
Юу 4.5 (УжДЙЄЮРбЄЮЖёТЮЮу)
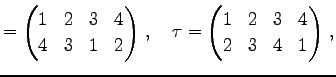 |
(600) | |
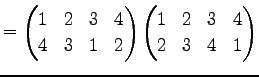 |
(601) | |
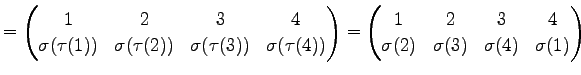 |
(602) | |
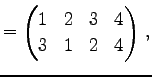 |
(603) | |
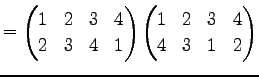 |
(604) | |
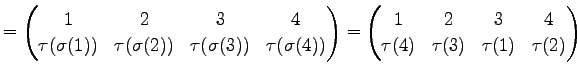 |
(605) | |
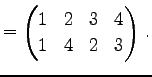 |
(606) |
УэАе 4.6 (УжДЙЄЮРбЄЯШѓВФДЙ)
АьШЬХЊЄЫ
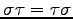 ЄЯРЎЮЉЄЗЄЪЄЄЁЅ
ЄЯРЎЮЉЄЗЄЪЄЄЁЅ
ФъЕС 4.7 (УБАЬУжДЙ)
СДЄЦЄЮЪИЛњЄђЦАЄЋЄЕЄЪЄЄУжДЙ
ЄђУБАЬУжДЙЄШИЦЄжЁЅ
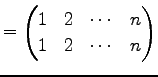 |
(607) |
ЄђУБАЬУжДЙЄШИЦЄжЁЅ
ФъЕС 4.8 (ЕеУжДЙ)
УжДЙ 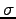 ЄЫТаЄЗЄЦ
ЄЫТаЄЗЄЦ
ЄђЫўЄПЄЙУжДЙ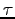 Єђ
Єђ 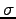 ЄЮЕеУжДЙЄШИЦЄгЁЄ
ЄЮЕеУжДЙЄШИЦЄгЁЄ
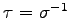 ЄШЩНЄяЄЙЁЅ
ЄШЩНЄяЄЙЁЅ
| (608) |
ЄђЫўЄПЄЙУжДЙ
ФъЭ§ 4.9 (ЕеУжДЙ)
УжДЙ
ЄЮЕеУжДЙЄЯ
ЄЧЭПЄЈЄщЄьЄыЁЅ
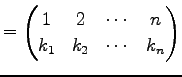 |
(609) |
ЄЮЕеУжДЙЄЯ
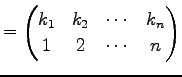 |
(610) |
ЄЧЭПЄЈЄщЄьЄыЁЅ
Юу 4.10 (ЕеУжДЙЄЮЖёТЮЮу)
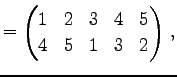 |
(611) | |
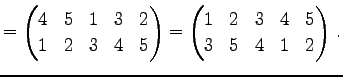 |
(612) |
ФъЕС 4.11 (НфВѓУжДЙ)
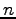 ИФЄЮЪИЛњ
ИФЄЮЪИЛњ
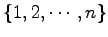 ЄЮЄІЄС
ЄЮЄІЄС
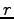 ИФЄЮЪИЛњ
ИФЄЮЪИЛњ
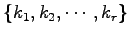 ЄЮЄпЄђ
ЄЮЄпЄђ
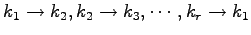 ЄШНчЄЫЄКЄщЄЗЁЄ
ЛФЄъЄЮЪИЛњ
ЄШНчЄЫЄКЄщЄЗЁЄ
ЛФЄъЄЮЪИЛњ
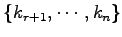 Єђ
Єђ
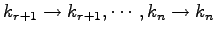 ЄШЦАЄЋЄЕЄЪЄЄ
МЬСќЄЮУжДЙЄђНфВѓУжДЙЄШЄЄЄІЁЅ
НфВѓУжДЙЄЯ
ЄШЦАЄЋЄЕЄЪЄЄ
МЬСќЄЮУжДЙЄђНфВѓУжДЙЄШЄЄЄІЁЅ
НфВѓУжДЙЄЯ
ЄШЩНЄяЄЕЄьЁЄОЪЮЌЄЙЄыЄШЄЄЯ
ЄШНёЄЏЁЅ
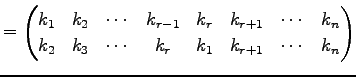 |
(613) | |
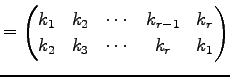 |
(614) |
ЄШЩНЄяЄЕЄьЁЄОЪЮЌЄЙЄыЄШЄЄЯ
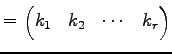 |
(615) |
ЄШНёЄЏЁЅ
Юу 4.12 (НфВѓУжДЙЄЮЖёТЮЮу)
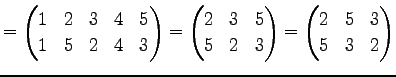 |
(616) | |
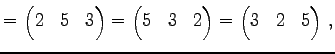 |
(617) | |
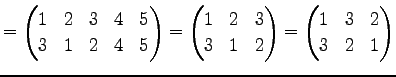 |
(618) | |
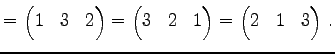 |
(619) |
ФъЭ§ 4.13 (УжДЙЄђНфВѓУжДЙЄЮРбЄЧЩНЄяЄЙ)
ЧЄАеЄЮУжДЙ 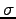 ЄЯНфВѓУжДЙ
ЄЯНфВѓУжДЙ
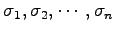 ЄЮРбЄЧ
ЄЮРбЄЧ
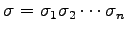 ЄШЩНЄяЄЕЄьЄыЁЅ
ЄШЩНЄяЄЕЄьЄыЁЅ
Юу 4.14 (УжДЙЄђНфВѓУжДЙЄЮРбЄЧЩНЄяЄЙЗзЛЛЮу)
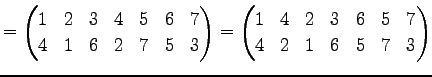 |
(620) | |
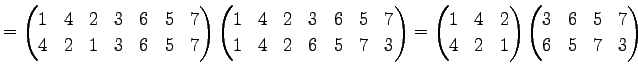 |
(621) | |
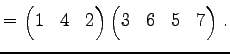 |
(622) |
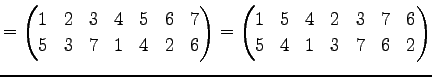 |
(623) | |
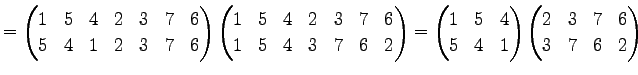 |
(624) | |
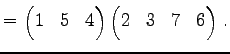 |
(625) |
ФъЕС 4.15 (ИпДЙ)
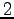 ЪИЛњЄЮНфВѓУжДЙ
ЪИЛњЄЮНфВѓУжДЙ
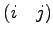 Єђ
ИпДЙЄШЄЄЄІЁЅ
Єђ
ИпДЙЄШЄЄЄІЁЅ
ФъЭ§ 4.16 (НфВѓУжДЙЄђИпДЙЄЮРбЄЧЩНЄяЄЙ)
ЧЄАеЄЮНфВѓУжДЙЄЯИпДЙЄЮРбЄЧЩНЄяЄЕЄьЄыЁЅ
ЄПЄШЄЈЄаЁЄЄНЄЮАьЄФЄШЄЗЄЦ
ЄШЩНЄяЄЕЄьЄыЁЅ
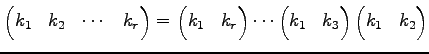 |
(626) |
ЄШЩНЄяЄЕЄьЄыЁЅ
Юу 4.17 (УжДЙЄђИпДЙЄЮРбЄЧЩНЄяЄЙ)
ЄПЄШЄЈЄа
ЄПЄШЄЈЄа
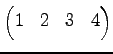 |
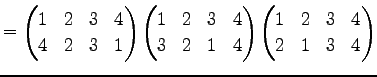 |
(627) |
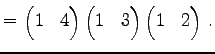 |
(628) |
ЄПЄШЄЈЄа
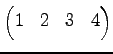 |
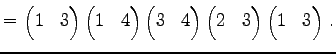 |
(629) |
УэАе 4.18
ИпДЙЄЮРбЄЧЩНЄяЄЙЪ§ЫЁЄЯДіФЬЄъЄтЄЂЄыЁЅ
ФъЕС 4.19 (УжДЙЄЮЩфЙц)
УжДЙ 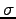 ЄЌ
ЄЌ 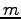 ИФЄЮИпДЙЄЮРбЄЧЩНЄяЄЕЄьЄыЄШЄ
ИФЄЮИпДЙЄЮРбЄЧЩНЄяЄЕЄьЄыЄШЄ
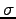 ЄЮЩфЙцЁЪsignЁЫЄђ
ЄЮЩфЙцЁЪsignЁЫЄђ
ЄШФъЕСЄЙЄыЁЅ
| (630) |
ЄШФъЕСЄЙЄыЁЅ
Юу 4.20 (УжДЙЄЮЩфЙцЄЮЖёТЮЮу)
ЄшЄъ
ЄШЄЪЄыЁЅЄоЄП
ЄшЄъ
ЄЧЄЂЄыЁЅ
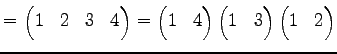 |
(631) |
ЄшЄъ
| (632) |
ЄШЄЪЄыЁЅЄоЄП
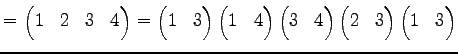 |
(633) |
ЄшЄъ
| (634) |
ЄЧЄЂЄыЁЅ
ФъЭ§ 4.21 (УжДЙЄЮЩфЙцЄЮАьАеР)
УжДЙ 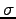 ЄЮЩфЙц
ЄЮЩфЙц
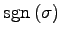 ЄЯ
ИпДЙЄЮРбЄЮЩНЄяЄЗЪ§ЄЫЄшЄщЄКАьАеЄЫФъЄоЄыЁЅ
ЄЯ
ИпДЙЄЮРбЄЮЩНЄяЄЗЪ§ЄЫЄшЄщЄКАьАеЄЫФъЄоЄыЁЅ
ФъЭ§ 4.22 (УжДЙЄЮЩфЙцЄЮРМС)
| (635) | ||
| (636) | ||
| (637) |
ФъЕС 4.23 (ЖіУжДЙЁЄДёУжДЙ)
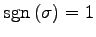 ЄШЄЪЄыУжДЙЄђ
ЖіУжДЙЄШИЦЄгЁЄ
ЄШЄЪЄыУжДЙЄђ
ЖіУжДЙЄШИЦЄгЁЄ
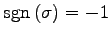 ЄШЄЪЄыУжДЙЄђ
ДёУжДЙЄШИЦЄжЁЅ
ЄШЄЪЄыУжДЙЄђ
ДёУжДЙЄШИЦЄжЁЅ
Юу 4.24 (ЖіУжДЙЁЄДёУжДЙЄЮЖёТЮЮу)
ЄшЄъ
ЄШЄЪЄыЁЅ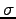 ЄЯЖіУжДЙЄЧЄЂЄыЁЅ
ЄЯЖіУжДЙЄЧЄЂЄыЁЅ
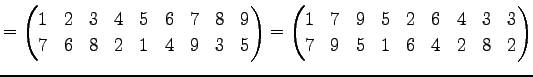 |
(638) | |
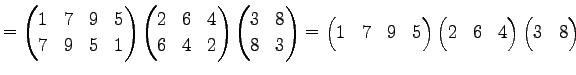 |
(639) | |
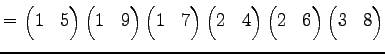 |
(640) |
ЄшЄъ
| (641) |
ЄШЄЪЄыЁЅ
ФъЕС 4.25 (УжДЙСДТЮЄЮНИЙч)
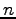 ЪИЛњЄЮУжДЙ
ЪИЛњЄЮУжДЙ 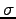 ЄЮСДТЮЄЮНИЙчЄђ
ЄЮСДТЮЄЮНИЙчЄђ 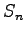 ЄШНёЄЏЁЅ
ЄШНёЄЏЁЅ
УэАе 4.26 (УжДЙСДТЮЄЮНИЙчЄЮЭзСЧЄЮИФПє)
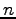 ЪИЛњЄЮУжДЙЄЯМЬСќ
ЪИЛњЄЮУжДЙЄЯМЬСќ
ЄЧЄЂЄыЄЋЄщЁЄ ЄНЄЮИФПєЄЯ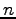 ИФЄЮЪИЛњЄЮНчЮѓСШЙчЄяЄЛЄЫХљЄЗЄЄЁЅ
ЄшЄУЄЦНИЙч
ИФЄЮЪИЛњЄЮНчЮѓСШЙчЄяЄЛЄЫХљЄЗЄЄЁЅ
ЄшЄУЄЦНИЙч 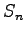 ЄЮИФПєЄЯ
ЄЮИФПєЄЯ 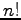 ЄЧЄЂЄыЁЅ
ЄЧЄЂЄыЁЅ
| (642) |
ЄЧЄЂЄыЄЋЄщЁЄ ЄНЄЮИФПєЄЯ
Юу 4.27 (УжДЙСДТЮЄЮНИЙчЄЮЖёТЮЮу)
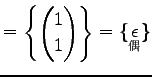 |
(643) | |
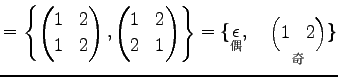 |
(644) | |
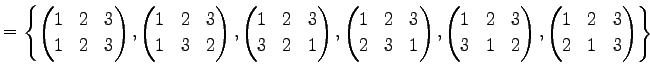 |
(645) | |
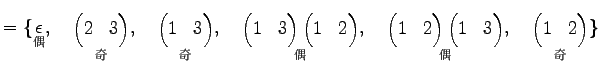 |
(646) |
Ьф 4.28 (УжДЙСДТЮЄЮНИЙч)
 МЁЄЮУжДЙСДТЮЄЮНИЙч
МЁЄЮУжДЙСДТЮЄЮНИЙч  ЄЮЭзСЧСДЄЦЄђНёЄНаЄЛЁЅ
ЄоЄПЄНЄЮЖіДёЄтНвЄйЄшЁЅ
ЄЮЭзСЧСДЄЦЄђНёЄНаЄЛЁЅ
ЄоЄПЄНЄЮЖіДёЄтНвЄйЄшЁЅ
Ьф 4.29 (ЖіУжДЙЁЄДёУжДЙЄЮИФПє)
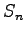
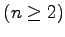 ЄЫДоЄоЄьЄыЖіУжДЙЄШДёУжДЙЄЮИФПєЄЯХљЄЗЄЄЁЅ
ЄГЄьЄђМЈЄЛЁЅ
ЄЫДоЄоЄьЄыЖіУжДЙЄШДёУжДЙЄЮИФПєЄЯХљЄЗЄЄЁЅ
ЄГЄьЄђМЈЄЛЁЅ
ЪПРЎ20ЧЏ2Зю2Цќ