5.35 ジョルダン標準形
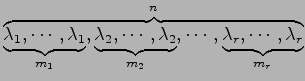
行列 ![]() のある固有値
のある固有値 ![]() の重複度が
の重複度が ![]() であるとする.
固有空間
であるとする.
固有空間
が
で定義される一般固有空間を考える.
が成り立つので,
定理 5.121 (一般固有空間)
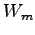 の基底で
の基底で
をみたす基底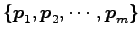 が存在する.また,
が存在する.また,
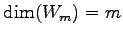 が成り立つ.
が成り立つ.
 |
||
をみたす基底
行列
![]() に対しては,この定理より
に対しては,この定理より
となり,
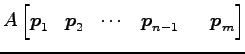 |
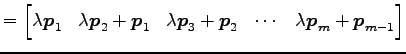 |
|
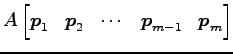 |
![$\displaystyle = \begin{bmatrix}\vec{p}_1 & \vec{p}_2 & \cdots & \vec{p}_{m-1} &...
...bda & \ddots \\ [-1ex] & & & \ddots & 1 \\ [-1ex] & & & & \lambda \end{bmatrix}$](img3551.png) |
|
が成り立つ. 一般には次の定理が成り立つ.
定理 5.122
行列 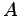 は固有値
は固有値
をもつとする. このとき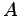 はある正則行列
はある正則行列 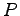 を用いて
を用いて
の形にブロック対角化される.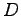 をジョルダン標準形(Jordan canonical form)という.
ここで
をジョルダン標準形(Jordan canonical form)という.
ここで
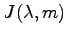 を
ジョルダンブロック(Jordan block)または
ジョルダン細胞(Jordan cell)という.
を
ジョルダンブロック(Jordan block)または
ジョルダン細胞(Jordan cell)という.
 |
をもつとする. このとき
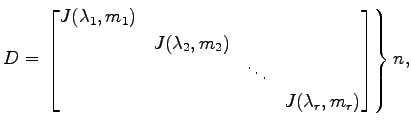 |
||
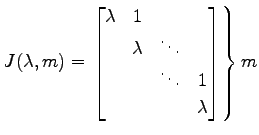 |
の形にブロック対角化される.
例 5.123 (ジョルダン標準形の具体例)
行列
を対角化する.
より,固有値は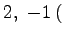 2 重
2 重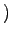 となる.
となる.
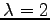 のとき,
のとき,
となるので,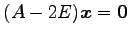 を解いて
固有ベクトルは
を解いて
固有ベクトルは
と得られる.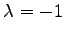 のとき,
のとき,
となるので,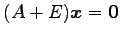 を解いて
固有ベクトルは
を解いて
固有ベクトルは
と得られる.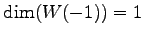 であり対角化できない.
であり対角化できない.
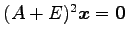 の解空間である
一般固有空間
の解空間である
一般固有空間 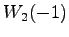 を考える.
このとき,
を考える.
このとき,
より,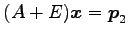 を解いて
を解いて
となるので,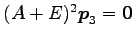 ,
,
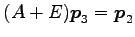 をみたす
一般固有ベクトル
をみたす
一般固有ベクトル 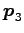 が得られる.
このとき
が得られる.
このとき 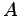 はジョルダン標準形に
はジョルダン標準形に
と分解される.
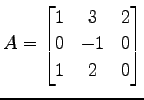 |
を対角化する.
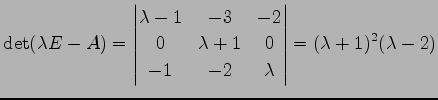 |
より,固有値は
 |
となるので,
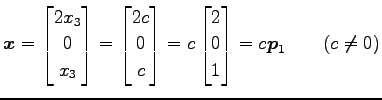 |
と得られる.
 |
となるので,
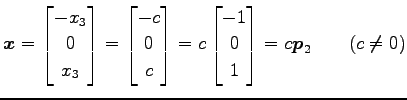 |
と得られる.
![$\displaystyle [A+E\,\,\vert\,\,\vec{p}_2] = \begin{bmatrix}2 & 3 & 2 & -1 \\ 0 ...
...d \begin{bmatrix}1 & 0 & 1 & -5 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 0 & 0 \end{bmatrix}$](img3567.png) |
より,
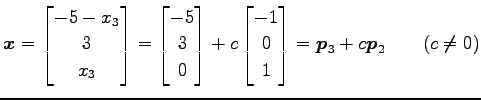 |
となるので,
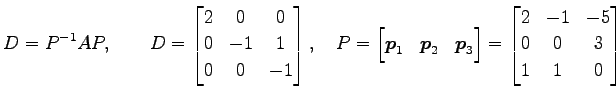 |
と分解される.
問 5.124 (ジョルダン標準形)
数値を代入し
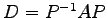 が成り立つことを確認せよ.
が成り立つことを確認せよ.
問 5.125 (ジョルダン標準形)
に対して
が成り立つことを示せ.
![$\displaystyle J= \begin{bmatrix}\lambda & 1 \\ [-1ex] & \lambda & \ddots \\ [-1ex] & & \ddots & 1 \\ [-1ex] & & & \lambda \end{bmatrix}$](img3573.png) |
に対して
![$\displaystyle J^k= \begin{bmatrix}\lambda^k & k\lambda^{k-1} \\ [-1ex] & \lambd...
...s \\ [-1ex] & & \ddots & k\lambda^{k-1} \\ [-1ex] & & & \lambda^k \end{bmatrix}$](img3574.png) |
が成り立つことを示せ.
平成20年2月2日