2.1 数ベクトル空間
定義 2.1 (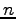 次元実ベクトル空間)
要素が実数の列ベクトル全体の集合
次元実ベクトル空間)
要素が実数の列ベクトル全体の集合
に次の演算(i)スカラー倍(scalar product), (ii)ベクトルの和が定義されているとき,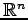 を
を
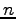 次元実ベクトル空間
(
次元実ベクトル空間
(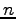 -dimensional real vector space)という.
-dimensional real vector space)という.
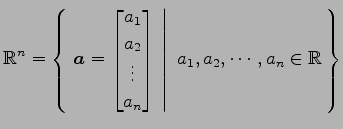 |
に次の演算(i)スカラー倍(scalar product), (ii)ベクトルの和が定義されているとき,
(i)
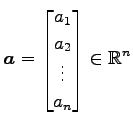 ,
,
![]() に対して,
に対して,
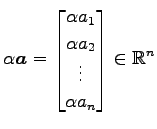 .
.
(ii)
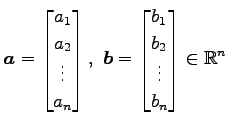 に対して,
に対して,
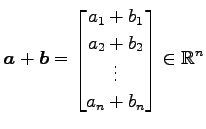 .
.
定義 2.2 (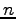 次元複素ベクトル空間)
要素が複素数の列ベクトル全体の集合
次元複素ベクトル空間)
要素が複素数の列ベクトル全体の集合
に次の演算(i)スカラー倍, (ii)ベクトルの和が定義されているとき,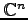 を
を
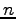 次元複素ベクトル空間
(
次元複素ベクトル空間
(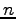 -dimensional complex vector space)という.
-dimensional complex vector space)という.
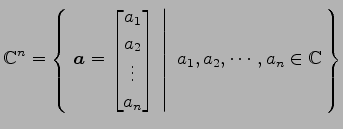 |
に次の演算(i)スカラー倍, (ii)ベクトルの和が定義されているとき,
(i)
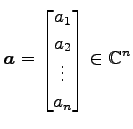 ,
,
![]() に対して,
に対して,
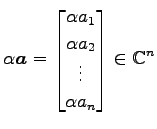 .
.
(ii)
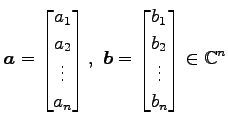 に対して,
に対して,
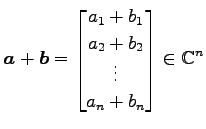 .
.
定義 2.3 (数ベクトル空間)
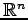 ,
,
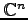 を
数ベクトル空間(number vector space)という.
を
数ベクトル空間(number vector space)という.
平成20年2月2日