1.3 集合算
定義 1.9 (和,積)
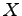 と
と 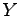 の合併集合(union, join)または
和集合(sum):
の合併集合(union, join)または
和集合(sum):
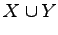
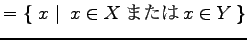
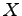 と
と 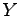 の共通部分(intersection)または
積集合(product):
の共通部分(intersection)または
積集合(product):
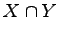
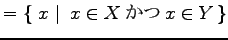
定理 1.10 (和集合,積集合の性質)
- 可換則(commutative law):

- 結合則(associative law):
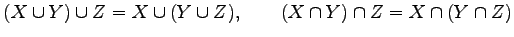
- 分配則(distributive law):
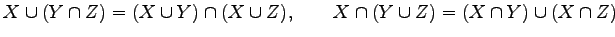
- 吸収則(absorption law):
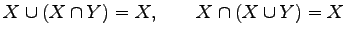
問 1.11 (和集合,積集合の性質)
これを図を書いて示せ.
定義 1.12 (互いに素)
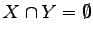 のとき
のとき 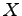 と
と 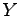 は
互いに素(disjoint)であるという.
は
互いに素(disjoint)であるという.
注意 1.13 (直和集合)
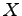 と
と 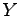 が互いに素のとき,
すなわち
が互いに素のとき,
すなわち
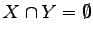 をみたすとき,
和集合を
をみたすとき,
和集合を
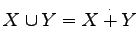 と書き,
直和集合(disjoint union)という.
と書き,
直和集合(disjoint union)という.
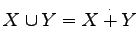 と書き,
直和集合(disjoint union)という.
と書き,
直和集合(disjoint union)という.
注意 1.14 (直積集合)
直積集合(direct product set, Cartesian product set):
平成20年2月2日