1.5 体の性質
定理 1.18 (体の性質)
体 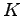 について次の条件が成り立つ:
について次の条件が成り立つ:
- (i).
- 零元 0,単位元
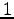 は唯一つに定まる.
は唯一つに定まる.
- (ii).
- 和の逆元
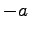 は各
は各 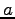 に対して唯一つに定まる.
に対して唯一つに定まる.
- (iii).
- 積の逆元
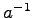 は各
は各 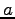 に対して唯一つに定まる.
に対して唯一つに定まる.
- (iv).
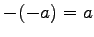 .
.
- (v).
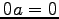 .
.
- (vi).
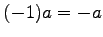 .
.
- (vii).
-
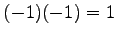 .
.
- (viii).
-
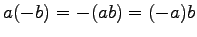 .
.
- (ix).
-
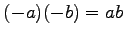 .
.
- (x).
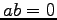
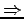
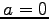 または
または 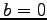 .
.
- (xi).
-
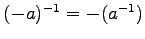 .
.
- (xii).
-
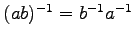 .
.
問 1.19 (零元,単位元,逆元の一意性)
これを示せ.
とする. この式は全ての元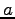 で成立するので,
第一式の
で成立するので,
第一式の 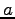 を
を 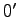 とし,
第二式の
とし,
第二式の 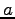 を 0 とすると
を 0 とすると
となる.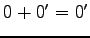 ,
, 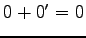 より,
より, 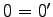 を得る.
零元は唯一つに定まる.
を得る.
零元は唯一つに定まる.
とする.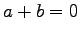 に左から
に左から 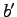 を加えると
を加えると
となる. 和の結合則より左辺の和の順を変える. 右辺は零元を加えているので
が成り立つ.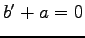 を用いると
を用いると
である.よって
を得る.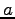 に対する和の逆元は唯一つに定まる.
に対する和の逆元は唯一つに定まる.
(証明)
(i)
零元が 0, ![]() と二つ存在するとする.
すなわち
と二つ存在するとする.
すなわち
とする. この式は全ての元
となる.
(ii)
![]() の和の逆元が
の和の逆元が ![]() ,
, ![]() と二つ存在するとする.
すなわち
と二つ存在するとする.
すなわち
とする.
となる. 和の結合則より左辺の和の順を変える. 右辺は零元を加えているので
が成り立つ.
である.よって
を得る.
(iii)は(ii)と同様に示される.他は自習とする.
平成20年2月2日