1.6 複素数
定義 1.20 (複素数)
複素数(complex number)とは,
実数 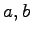 に対して
に対して 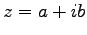 で定まる数である.
ただし
で定まる数である.
ただし 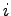 は
は 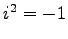 をみたし,
虚数単位(imaginary unit)と呼ぶ.
複素数
をみたし,
虚数単位(imaginary unit)と呼ぶ.
複素数 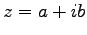 の
の 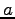 を実部(real part)といい
を実部(real part)といい
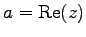 と表す.
と表す.
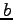 を虚部(imaginary part)といい
を虚部(imaginary part)といい
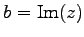 と表す.
虚部が
と表す.
虚部が
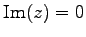 のとき
のとき
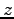 は実数(real number)といい,
実部が
は実数(real number)といい,
実部が
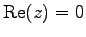 のとき
のとき 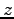 は
純虚数(pure imaginary number)という.
は
純虚数(pure imaginary number)という.
定義 1.21 (複素平面)
複素数全体の集合を
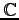 と表す.
この集合を実部
と表す.
この集合を実部
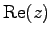 を横軸に
虚部
を横軸に
虚部
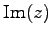 を縦軸にとることできる平面を
複素平面(complex plane)と呼ぶ.
このとき横軸を実軸(real axis)といい,
縦軸を虚軸(imaginary axis)という.
を縦軸にとることできる平面を
複素平面(complex plane)と呼ぶ.
このとき横軸を実軸(real axis)といい,
縦軸を虚軸(imaginary axis)という.
定義 1.22 (複素共役)
複素数 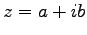 に対して複素数
に対して複素数
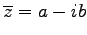 を
を
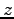 の複素共役(complex conjugate)という.
の複素共役(complex conjugate)という.
定義 1.23 (複素数の絶対値と偏角)
複素数 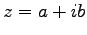 に対して実数
に対して実数
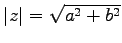 を
を
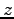 の絶対値(absolute value)
または大きさ(modulus)という.
の絶対値(absolute value)
または大きさ(modulus)という.
 を
を 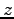 の
偏角(argument)という.
の
偏角(argument)という.
注意 1.24 (複素数の絶対値と偏角)
複素平面上で原点 0 とあるある複素数 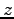 との距離は
との距離は 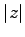 である.
また,実軸と 2 点 0,
である.
また,実軸と 2 点 0, 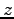 を通る直線とのなす角は
を通る直線とのなす角は 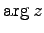 である.
である.
定理 1.25 (複素数の性質)
複素数 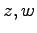 に対して次の性質が成り立つ:
に対して次の性質が成り立つ:
- (i).
-
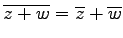 .
.
- (ii).
-
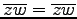 .
.
- (iii).
-
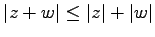 .
.
- (iv).
-
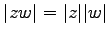 .
.
- (v).
-
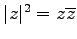 .
.
- (vi).
-
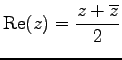 .
.
- (vii).
-
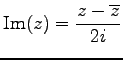 .
.
- (viii).
-
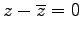
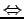
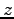 は実数.
は実数.
- (ix).
-
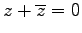
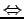
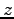 は純虚数.
は純虚数.
問 1.26 (複素数の性質)
これらの性質を示せ.
平成20年2月2日