4.1 線形写像
定義 4.1 (線形写像)
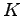 (
(
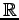 または
または
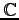 ) 上の
ベクトル空間
) 上の
ベクトル空間 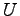 から
から 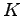 上のベクトル空間
上のベクトル空間  への写像
への写像
が次の条件(i), (ii)をみたすとき, を線形写像(linear mapping)
または1 次写像という.
を線形写像(linear mapping)
または1 次写像という.
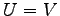 のとき
のとき  を
線形変換(linear transformation)または
1 次変換という.
を
線形変換(linear transformation)または
1 次変換という.
が次の条件(i), (ii)をみたすとき,
- (i).
-
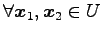 に対して,
に対して,
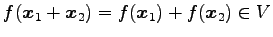 .
.
- (ii).
-
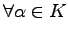 ,
,
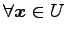 に対して,
に対して,
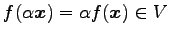 .
.
定理 4.2 (線形写像)
線形写像であるための必要十分条件は,
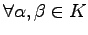 ,
,
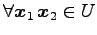 に対して,
に対して,
が成り立つことである.
が成り立つことである.
注意 4.3 (零ベクトル)
線形写像  は零ベクトル
は零ベクトル
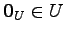 を
零ベクトル
を
零ベクトル
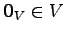 へ写す.
なぜなら,条件(ii)において
へ写す.
なぜなら,条件(ii)において 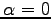 とすると
とすると
となるからである.
となるからである.
例 4.4 (線形写像の具体例)
写像
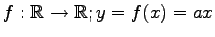 は線形写像である.
なぜなら,
は線形写像である.
なぜなら,
をみたすからである.
をみたすからである.
例 4.5 (線形写像)
写像
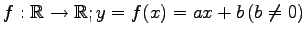 は
線形写像ではない.
なぜなら,条件(i)は
は
線形写像ではない.
なぜなら,条件(i)は
であり,条件(ii)は
となるからである.
であり,条件(ii)は
となるからである.
例 4.6 (線形写像)
写像
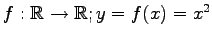 は線形写像ではない.
なぜなら,条件(i)は
は線形写像ではない.
なぜなら,条件(i)は
であり,条件(ii)は
となるからである.
であり,条件(ii)は
となるからである.
例 4.7 (線形写像の具体例)
写像
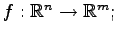
は線形写像である. なぜなら,
をみたすからである.
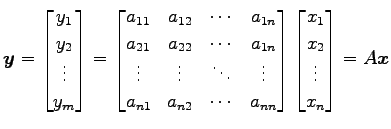 |
は線形写像である. なぜなら,
をみたすからである.
問 4.8 (線形写像)
次の写像は線形写像ではないことを示せ.
問 4.9 (線形写像の具体例)
写像
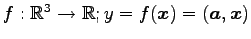 は
線形写像であることを示せ.
ただし,
は
線形写像であることを示せ.
ただし,
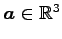 とする.
とする.
問 4.10 (線形写像の具体例)
 において
点
において
点  から
単位方向ベクトルが
から
単位方向ベクトルが 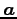 の直線に
垂直に下ろした点 tex2html_wrap_inline$y$ を正射影という.
この写像
の直線に
垂直に下ろした点 tex2html_wrap_inline$y$ を正射影という.
この写像
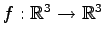 は
は
と表され,射影変換という. は線形変換である.
これを示せ.
は線形変換である.
これを示せ.
と表され,射影変換という.
問 4.11 (線形写像の具体例)
 において
点
において
点  から平面
から平面
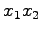 に
垂直に下ろした点 tex2html_wrap_inline$y$ を正射影という.
この写像
に
垂直に下ろした点 tex2html_wrap_inline$y$ を正射影という.
この写像
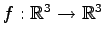 は
は
または,
と表され,射影変換という. は線形変換である.
これを示せ.
は線形変換である.
これを示せ.
または,
と表され,射影変換という.
まとめ 4.12 (線形写像)
- 線形写像は原点を原点へ写す.
- 平行移動をともなう写像は線形写像ではない.
- 線形写像は定数を含まない 1 次式である.
- 線形写像は平行四辺形を平行四辺形へ写す.
平成20年2月2日