4.2 演習問題 〜 線形写像
問 4.13 (線形写像)
次の変換
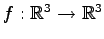 ;
;
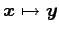 が
線形変換であるか否か示せ.
が
線形変換であるか否か示せ.
(1) 点 と原点
と原点 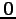 との中点
との中点  への変換.
への変換.
(2) 点 と点
と点
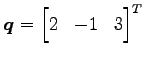 との中点
との中点  への変換.
への変換.
(3) 直線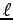 を原点
を原点 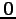 を通り方向ベクトル
を通り方向ベクトル
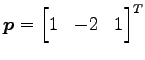 の
直線とする.
点
の
直線とする.
点  から直線
から直線 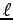 へ正射影
へ正射影  への変換.
への変換.
(4) 直線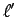 を点
を点 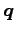 を通り
方向ベクトル
を通り
方向ベクトル 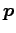 の直線とする.
点
の直線とする.
点  から直線
から直線 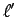 への正射影
への正射影  への変換.
への変換.
(5) 点 から直線
から直線 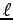 への正射影との中点
への正射影との中点  への変換.
への変換.
(6) 点 から直線
から直線 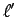 への正射影との中点
への正射影との中点  への変換.
への変換.
(7) 直線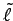 を原点
を原点 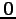 を通り方向ベクトル
を通り方向ベクトル
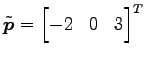 の
直線とする.
点
の
直線とする.
点  から直線
から直線 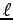 への正射影と
点
への正射影と
点  から直線
から直線
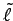 への正射影との
中点
への正射影との
中点  への変換.
への変換.
(8) 直線 を点
を点 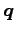 を通り
方向ベクトル
を通り
方向ベクトル
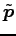 の直線とする.
点
の直線とする.
点  から直線
から直線 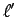 への正射影と
点
への正射影と
点  から直線
から直線
 への正射影との
中点
への正射影との
中点  への変換.
への変換.
(9)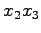 平面への正射影
平面への正射影  への変換.
(10)
平面
への変換.
(10)
平面 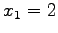 への正射影
への正射影  への変換.
への変換.
(11)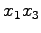 平面への正射影
平面への正射影  への変換.
(12)
平面
への変換.
(12)
平面 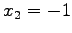 への正射影
への正射影  への変換.
への変換.
(13)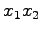 平面への正射影との中点
平面への正射影との中点  への変換.
への変換.
(14) 原点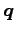 に関して点対称な点
に関して点対称な点  への変換.
への変換.
(15) 原点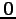 に関して点対称な点
に関して点対称な点  への変換.
への変換.
(16) 平面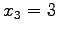 への正射影との中点
への正射影との中点  への変換.
への変換.
(17)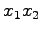 平面に関して対称な点
平面に関して対称な点  への変換.
への変換.
(18) 平面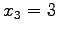 に関して対称な点
に関して対称な点  への変換.
への変換.
(19) 原点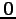 と点
と点  を通る直線上にあり,
原点
を通る直線上にあり,
原点 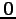 からの距離が
からの距離が 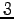 倍となる点
倍となる点  への変換.
への変換.
(20) 点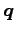 と点
と点  を通る直線上にあり,
点
を通る直線上にあり,
点 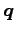 からの距離が
からの距離が 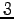 倍となる点
倍となる点  への変換.
への変換.
(1) 点
(2) 点
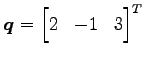 との中点
との中点 (3) 直線
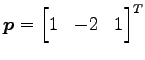 の
直線とする.
点
の
直線とする.
点 (4) 直線
(5) 点
(6) 点
(7) 直線
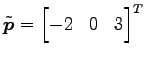 の
直線とする.
点
の
直線とする.
点 (8) 直線
(9)
(11)
(13)
(14) 原点
(15) 原点
(16) 平面
(17)
(18) 平面
(19) 原点
(20) 点
問 4.14 (線形写像)
次の写像は線形写像か否か示せ.
(1)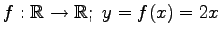 (2)
(2)
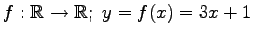
(3)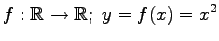 (4)
(4)
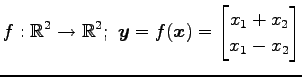
(5)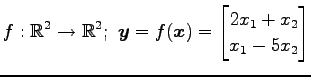 (6)
(6)
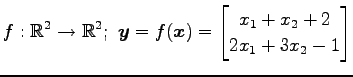
(7)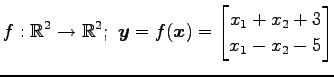 (8)
(8)
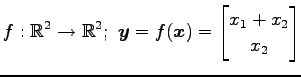
(9)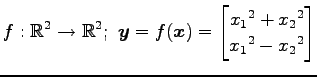 (10)
(10)
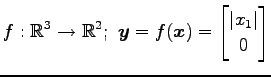
(11)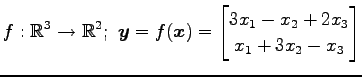 (12)
(12)
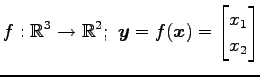
(13)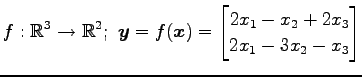 (14)
(14)
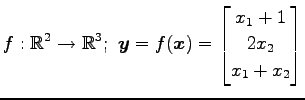
(15)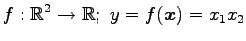 (16)
(16)
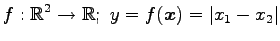
(17)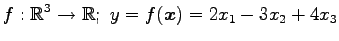 (18)
(18)
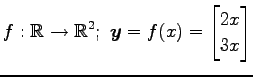
(19)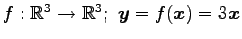 (20)
(20)
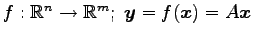 ,
ただし
,
ただし
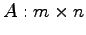 .
.
(21)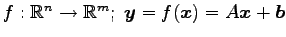 ,
ただし
,
ただし
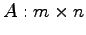 ,
,
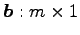 .
.
(22)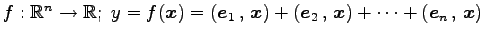
(23)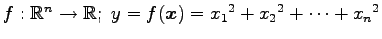
(24)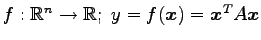 ,
ただし
,
ただし
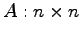 .
.
(1)
(3)
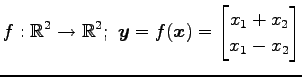
(5)
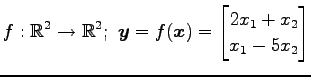 (6)
(6)
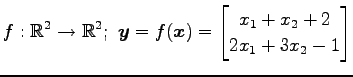
(7)
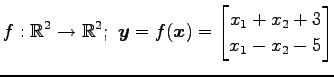 (8)
(8)
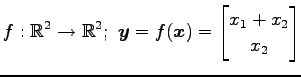
(9)
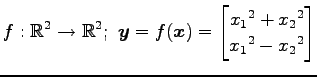 (10)
(10)
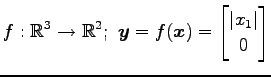
(11)
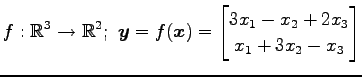 (12)
(12)
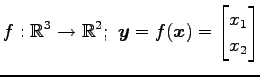
(13)
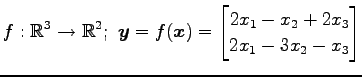 (14)
(14)
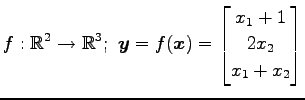
(15)
(17)
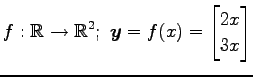
(19)
(21)
(22)
(23)
(24)
問 4.15 (線形写像)
次の変換
![$ F:\mathbb{R}[x]_2\to\mathbb{R}[x]_2$](img2093.png) ;
;
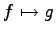 が
線形変換であるか否か示せ.
が
線形変換であるか否か示せ.
(1)
![]() (2)
(2)
![]()
(3)
![]() (4)
(4)
![]()
(5)
![]()
注意 4.16 (汎関数)
写像 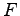 は入力が関数
は入力が関数 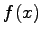 で
出力が関数
で
出力が関数 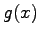 の関数とみなせる.
関数の関数のことを汎関数(functional)という.
の関数とみなせる.
関数の関数のことを汎関数(functional)という.
などと表記する.
などと表記する.
平成20年2月2日