4.3 線形写像の行列表示
定理 4.17 (線形写像の行列表示)
任意の線形写像
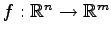 は
は
と行列表示が可能である. 行列 を
を  の
標準基底に関する表現行列という.
の
標準基底に関する表現行列という.
と行列表示が可能である. 行列
例 4.18 (線形写像の行列表示の具体例)
ある線形写像
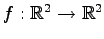 は
は
をみたす写像である. このとき の行列表示
の行列表示
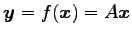 を求める.
を求める.
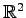 の任意のベクトルは
の任意のベクトルは
と表される. このとき
が成り立つ. よって の標準基底に関する表現行列
の標準基底に関する表現行列  は
は
である. の行列表示
の行列表示
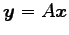 は
は
と得られる.
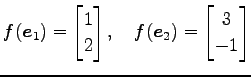 |
をみたす写像である. このとき
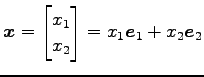 |
と表される. このとき
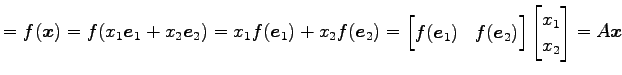 |
が成り立つ. よって
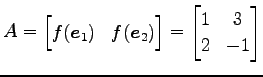 |
である.
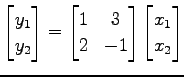 |
と得られる.
例 4.19 (線形写像の行列表示)
 における
における 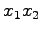 平面への
射影変換
平面への
射影変換
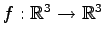 ;
;
の行列表示を求める. の任意のベクトル
の任意のベクトル
を で写すと,
で写すと,
と表される. ここで,標準基底を で写すと
で写すと
となる.これを用いると 標準基底に関する の表現行列は
の表現行列は
と求まる. あらためて行列表示を成分で表すと,
となる.また
とも書ける.
の行列表示を求める.
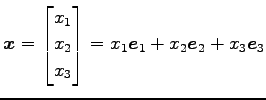 |
を
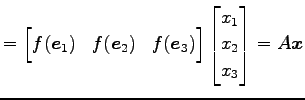 |
と表される. ここで,標準基底を
となる.これを用いると 標準基底に関する
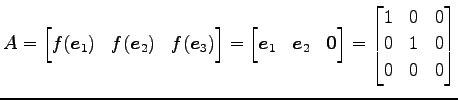 |
と求まる. あらためて行列表示を成分で表すと,
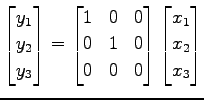 |
となる.また
とも書ける.
例 4.20 (行列表示の具体例)
ある線形写像
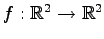 は
は
をみたす写像である. このとき の行列表示
の行列表示
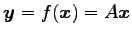 を求める.
を求める.
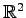 の任意のベクトル
の任意のベクトル  は標準基底
は標準基底
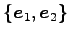 では
では
となり,基底
では
と表される. これは基底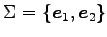 における
座標
における
座標
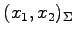 から
基底
から
基底
 における
座標
における
座標
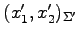 への
座標変換を表し,
への
座標変換を表し,
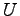 は基底の変換行列である.
また,この逆変換は
は基底の変換行列である.
また,この逆変換は
となる. これを用いて, 任意のベクトル を
を  で写すと
で写すと
と, の行列表示が得られる.
標準基底に関する表現行列
の行列表示が得られる.
標準基底に関する表現行列  は
は
となる. よって線形写像 の行列表示を成分であらためて表すと
の行列表示を成分であらためて表すと
となる.
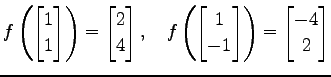 |
をみたす写像である. このとき
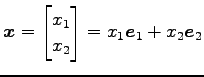 |
となり,基底
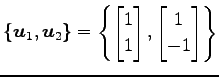 |
では
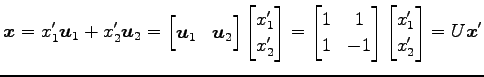 |
と表される. これは基底
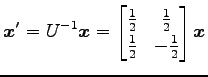 |
となる. これを用いて, 任意のベクトル
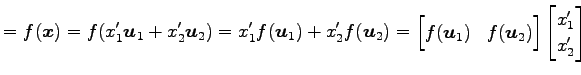 |
||
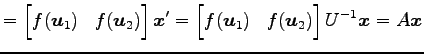 |
と,
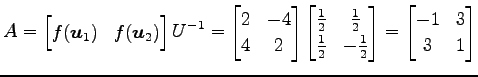 |
となる. よって線形写像
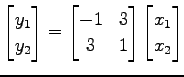 |
となる.
平成20年2月2日