4.23 点の平面への射影変換
例 4.104 (点の平面への射影)
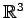 において,
任意の点
において,
任意の点
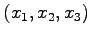 から平面
から平面
への射影変換 を求める.
方程式(☆)の一般解を求めると
を求める.
方程式(☆)の一般解を求めると
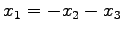 より
より
となる.平面(☆)は
と表せる. の基底
の基底
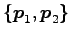 を
グラム・シュミットの直交化法で正規直交基底化する.
を
グラム・シュミットの直交化法で正規直交基底化する.
とおくと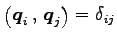 となる.
となる.
は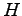 の正規直交基底となる.
ここで点
の正規直交基底となる.
ここで点
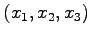 の位置ベクトルを
の位置ベクトルを 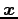 とし,
平面へ射影した点の位置ベクトルを
とし,
平面へ射影した点の位置ベクトルを 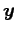 とおく.
射影点
とおく.
射影点 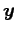 は平面
は平面 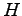 上にあるので,
基底
上にあるので,
基底
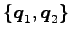 を用いて,
を用いて,
と表せる. このとき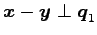 ,
,
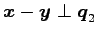 であり,
であり,
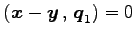 ,
,
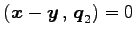 が成り立つ.
これより
が成り立つ.
これより
となり,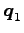 方向の座標は
方向の座標は
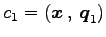 と得られる.
と得られる.
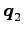 方向の座標も
同様にして
方向の座標も
同様にして
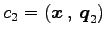 と得られる.
よって射影点は
と得られる.
よって射影点は
となる. 射影変換 が
が
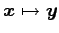 と得られた.
と得られた.
であり,これを で写すと
で写すと
となる. ここで,
より,
と行列表示を得る. の標準基底における表現行列は
の標準基底における表現行列は
となる.![\includegraphics[width=0.4\textwidth]{heimen-shaei.eps}](img2731.png)
への射影変換
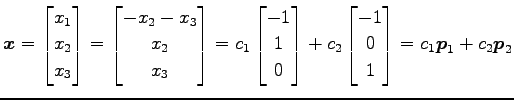 |
となる.平面(☆)は
と表せる.
 |
とおくと
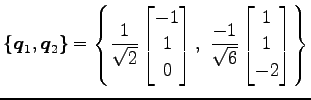 |
は
と表せる. このとき
となり,
となる. 射影変換
![]() を行列表示する.
を行列表示する.
![]() の任意の点
の任意の点 ![]() を標準基底
を標準基底
![]() で表すと,
で表すと,
であり,これを
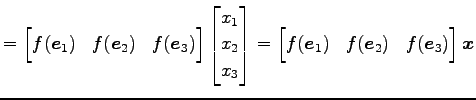 |
となる. ここで,
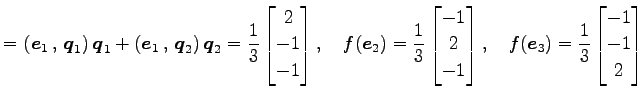 |
より,
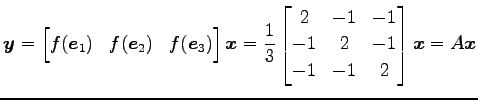 |
と行列表示を得る.
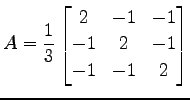 |
となる.
![\includegraphics[width=0.4\textwidth]{heimen-shaei.eps}](img2731.png)
問 4.105 (射影変換の像と階数)
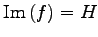 ,
,
 となることを示せ.
となることを示せ.
問 4.106 (射影変換の格と退化次数)
平面(☆)の法線ベクトルは
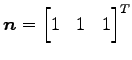 である.
である.
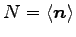 とおく.
とおく.
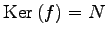 ,
,
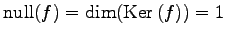 となることを示せ.
となることを示せ.
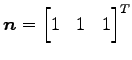 である.
である.
注意 4.107 (射影変換の正則性)
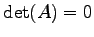 であり
であり 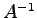 は存在しない.
よって射影変換
は存在しない.
よって射影変換  は正則変換ではない.
例えば
は正則変換ではない.
例えば
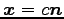 (
(
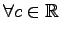 )
に対して
)
に対して
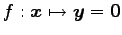 となる.
直線上のすべての点が原点
となる.
直線上のすべての点が原点 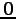 に写されるので,
逆元
に写されるので,
逆元
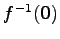 は存在しない.
は存在しない.
問 4.108 (射影変換の表現行列とべき等行列)
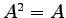 が成り立つことを示せ.
が成り立つことを示せ.
注意 4.109 (射影変換の表現行列とべき等行列)
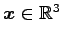 に対して射影変換
に対して射影変換  を作用させると,
を作用させると,
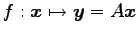 となる.
となる.
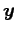 は平面
は平面 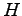 上にあり
上にあり
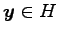 である.
である.
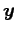 に対してさらに
に対してさらに  を作用させると
を作用させると
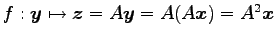 となる.
となる.
 は既に平面
は既に平面  上にあるので
上にあるので  により動かない.
よって
により動かない.
よって
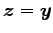 であるから,
であるから,
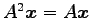 となる.
任意の
となる.
任意の 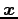 に対して成り立つので,
に対して成り立つので,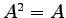 を得る.
を得る.
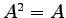 をみたす行列をべき等行列という.
一般にべき等行列を表現行列にもつ線形変換は射影変換となる.
をみたす行列をべき等行列という.
一般にべき等行列を表現行列にもつ線形変換は射影変換となる.
注意 4.110 (射影変換における直交補空間)
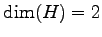 ,
, 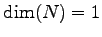 であることと,
であることと,
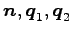 が 1 次独立であり
が 1 次独立であり
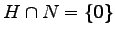 となることから,
となることから,
を得る. さらに,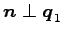 ,
,
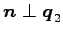 であるから,
であるから,
 と
と 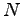 は互いに
は互いに
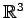 における直交補空間となる.
における直交補空間となる.
である.
を得る. さらに,
である.
注意 4.111 (射影変換の固有値空間)
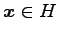 のとき,
のとき,
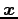 は既に平面
は既に平面 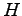 上にあるので,
射影変換
上にあるので,
射影変換  により動くことはない.
すなわち,
により動くことはない.
すなわち,
が成り立つ. これは固有値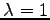 の
固有方程式
の
固有方程式
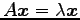 とみなせる.
または,
変換
とみなせる.
または,
変換  により
ベクトル
により
ベクトル 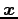 のスカラー
のスカラー 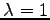 倍に写されるともみなせる.
すべての
倍に写されるともみなせる.
すべての
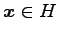 に対して成り立つので,
に対して成り立つので,
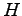 は固有空間
は固有空間 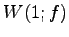 と等しい.
また,
と等しい.
また,
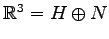 より
より
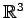 は
は
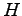 と
と 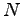 に直和分解される.
に直和分解される.
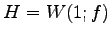 であるから,
であるから,
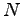 も固有空間
も固有空間
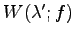 となる(はずである).
となる(はずである).
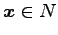 のとき,
平面
のとき,
平面 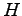 の原点
の原点 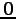 を通る法線上に
を通る法線上に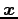 があるので,
があるので,
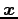 は
射影変換
は
射影変換  により原点
により原点 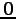 に写される.
これは,
変換
に写される.
これは,
変換  により
ベクトル
により
ベクトル 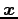 のスカラー
のスカラー
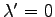 倍に写されるともみなせる.
よって,
倍に写されるともみなせる.
よって,
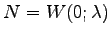 となる(はずである).
となる(はずである).
が成り立つ. これは固有値
問 4.112 (射影変換の固有値空間)
 の固有空間を具体的に求めて,
の固有空間を具体的に求めて,
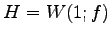 ,
, 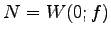 が成り立つことを示せ.
が成り立つことを示せ.
平成20年2月2日