4.22 演習問題 〜 直交変換
問 4.95 (直交行列)
次の行列は直交行列であることを示せ.
(1)
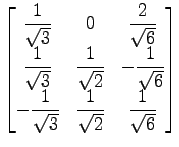 (2)
(2)
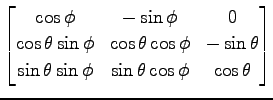
問 4.96 (直交行列)
次の行列が直交行列となるように 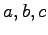 を定めよ.
を定めよ.
(1)
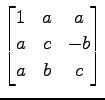 (2)
(2)
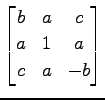 (3)
(3)
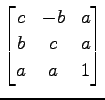 (4)
(4)
 (5)
(5)
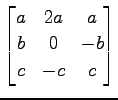
問 4.97 (直交行列)
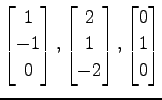
次のベクトルを正規直交化し,
列ベクトルにならべて直交行列を作れ.
(1)
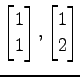 (2)
(2)
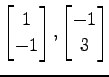 (3)
(3)
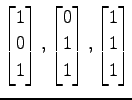 (4)
(4)
問 4.98 (回転行列)
回転行列
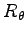 を
を
とする.次の関係式を示せ.
(1)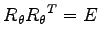 (2)
(2)
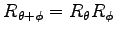 (3)
(3)
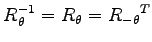
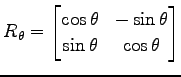 |
とする.次の関係式を示せ.
(1)
問 4.99 (回転変換)
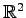 のベクトル
のベクトル
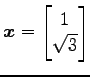 を原点を中心に反時計回りに
を原点を中心に反時計回りに
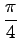 ,
,
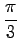 ,
,
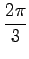 ,
,
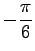 回転させた
ベクトル
回転させた
ベクトル  をそれぞれ求めよ.
また,変換
をそれぞれ求めよ.
また,変換
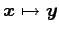 の表現行列をそれぞれ求めよ.
の表現行列をそれぞれ求めよ.
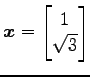 を原点を中心に反時計回りに
を原点を中心に反時計回りに
問 4.100 (鏡映変換)
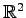 のベクトル
のベクトル
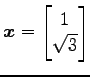 を
直線
を
直線 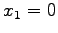 ,
, 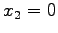 ,
, 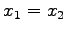 ,
, 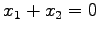 ,
,
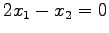 に対して鏡映変換したベクトル
に対して鏡映変換したベクトル  (
( と
と  は直線に対して線対称)をそれぞれ求めよ.
また,変換
は直線に対して線対称)をそれぞれ求めよ.
また,変換
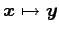 の表現行列をそれぞれ求めよ.
の表現行列をそれぞれ求めよ.
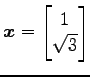 を
直線
を
直線
問 4.101 (鏡映変換)
次の行列による線形変換
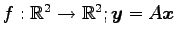 は
ある直線に対する鏡映変換である.
対称軸の直線の方程式を求めよ.
は
ある直線に対する鏡映変換である.
対称軸の直線の方程式を求めよ.
(1)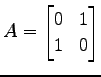 (2)
(2)
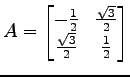
(1)
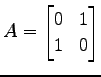 (2)
(2)
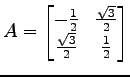
問 4.102 (回転行列と鏡映変換)
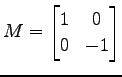 は
は 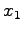 軸に対する鏡映変換行列である.
このとき,次の関係式をみたす
軸に対する鏡映変換行列である.
このとき,次の関係式をみたす 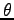 を定めよ.
を定めよ.
(1)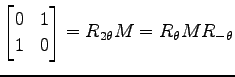 (2)
(2)
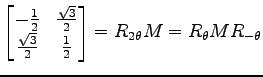
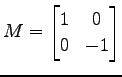 は
は (1)
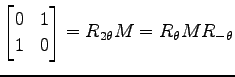 (2)
(2)
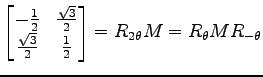
問 4.103 (回転行列と鏡映変換)
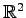 のベクトル
のベクトル
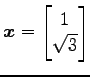 を原点を中心に反時計回りに
を原点を中心に反時計回りに
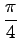 回転したベクトルを
回転したベクトルを  とする.
とする.
 を
を 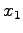 軸に対して鏡映変換したベクトルを
軸に対して鏡映変換したベクトルを 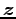 とする.
とする.
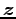 を
を
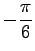 回転したベクトルを
回転したベクトルを 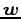 とする.
とする.
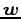 を直線
を直線 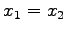 に対して
鏡映変換したベクトルを
に対して
鏡映変換したベクトルを 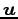 とする.
とする.
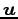 を
を
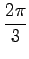 回転したベクトルを
回転したベクトルを 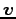 とする.
このとき,ベクトル
とする.
このとき,ベクトル  ,
, 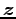 ,
, 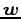 ,
,
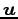 ,
, 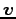 を求めよ.
また,変換
を求めよ.
また,変換
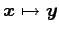 ,
,
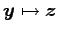 ,
,
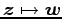 ,
,
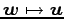 ,
,
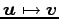 ,
,
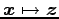 ,
,
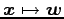 ,
,
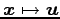 ,
,
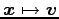 の標準基底に関する表現行列をそれぞれ求めよ.
さらに,この表現行列が直交行列であることを示せ.
の標準基底に関する表現行列をそれぞれ求めよ.
さらに,この表現行列が直交行列であることを示せ.
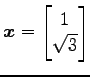 を原点を中心に反時計回りに
を原点を中心に反時計回りに
平成20年2月2日