6.18 定積分の性質
定理 6.85 (定積分の性質)
定積分は次の性質をもつ:
(5) 分割は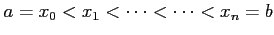 のままだが,
矩形の底辺に向きを与える.
これを
のままだが,
矩形の底辺に向きを与える.
これを
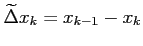 とおく.
このとき,
とおく.
このとき,
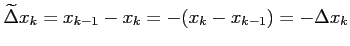 が成り立つ.
よって,
が成り立つ.
よって,
- (1)
-
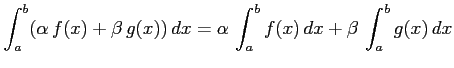 .
.
- (2)
-
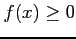
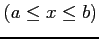 のとき
のとき
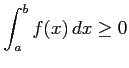 .
.
- (3)
-
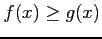
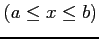 のとき
のとき
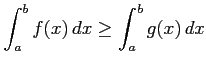 .
.
- (4)
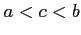 のとき
のとき
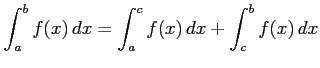 .
.
- (5)
-
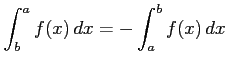 .
.
- (6)
-
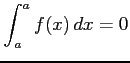 .
.
- (7)
-
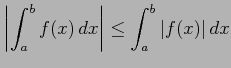
(証明)
(1)
![]() .
.
(2)
![]() .
.
(3)
![]() .
.
(4)
分割を
![]() とおき,
とおき,
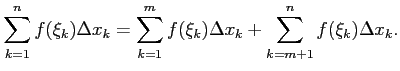 |
(5) 分割は
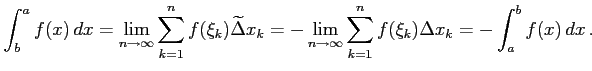 |
(6) 底辺の長さが 0 なので,面積は明らかに 0.
(7)
![]() .
.
定理 6.86 (中間値の定理)
関数 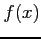 が区間
が区間 ![$ [a,b]$](img62.png) で連続で
で連続で
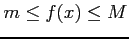 であるとき,
であるとき,
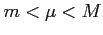 をみたす任意の
をみたす任意の 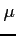 に対して,
に対して,
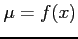 となる点
となる点 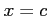 (
(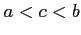 ) が存在する.
) が存在する.
定理 6.87 (定積分の性質)
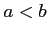 に対して
に対して
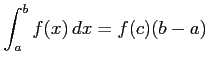 をみたす
をみたす 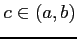 が存在する.
が存在する.
が成り立つ.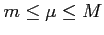 ,
,
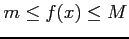 より中間値の定理より
より中間値の定理より
をみたす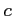 が存在する.
が存在する.
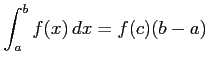 をみたす
をみたす
(証明)
![]() のとき
のとき
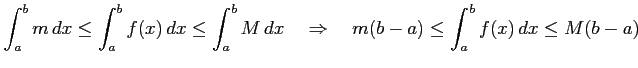 |
||
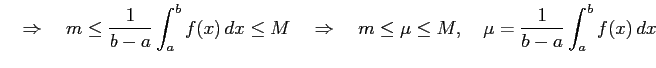 |
が成り立つ.
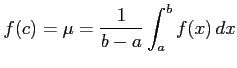 |
をみたす
平成21年6月1日