6.19 定積分と不定積分
定理 6.88 (定積分と不定積分の関係)
定積分
に対して
が成り立つ.
をみたす.全辺を区間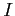 で定積分すれば,
で定積分すれば,
が成り立つ. 中辺は
となるので,不等式は
となる.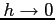 の極限においては
の極限においては
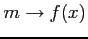 ,
, 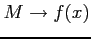 ,
,
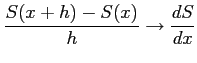 であるから,
であるから,
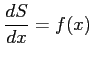 を得る.
を得る.
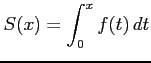 |
に対して
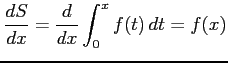 |
が成り立つ.
(証明)
関数 ![]() は連続関数であれば区間
は連続関数であれば区間 ![]() において
において
をみたす.全辺を区間
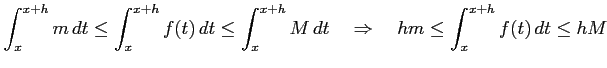 |
||
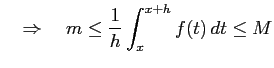 |
が成り立つ. 中辺は
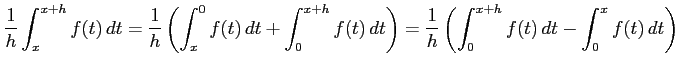 |
||
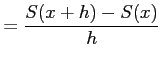 |
となるので,不等式は
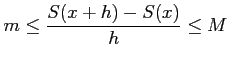 |
となる.
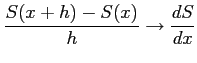 であるから,
であるから,
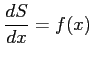 を得る.
を得る.
注意 6.89 (定積分と不定積分の関係)
関数 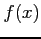 の不定積分から得られる原始関数の一つを
の不定積分から得られる原始関数の一つを 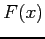 とすると,
とすると,
が成り立つ. 面積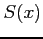 は
は 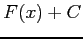 で与えられるが,
実際上は
で与えられるが,
実際上は 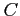 には任意性があるため,
この式では
には任意性があるため,
この式では 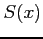 の値は定まらない.
の値は定まらない.
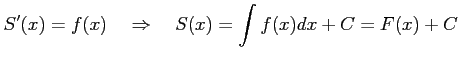 |
が成り立つ. 面積
定理 6.90 (定積分と不定積分の関係)
関数 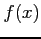 の不定積分から得られる原始関数の一つを
の不定積分から得られる原始関数の一つを
とする.このとき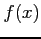 の
の 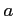 から
から 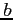 までの定積分は
までの定積分は
と表される.
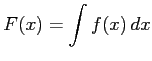 |
とする.このとき
![$\displaystyle \int_{a}^{b}f(x)dx=F(b)-F(a)= \Big[F(x)\Big]_{a}^{b}=F(x)\Big\vert _{x=a}^{x=b}$](img3277.png) |
と表される.
(証明)
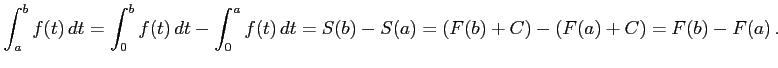 |
例 6.91 (定積分の計算例)
これは長方形の面積を表す.
![$\displaystyle \int_{a}^{b}\alpha\,dx= \alpha\int_{a}^{b}\,dx= \alpha\Big[x\Big]_{a}^{b}= \alpha(b-a)\,.$](img3279.png) |
これは長方形の面積を表す.
例 6.92 (定積分の計算例)
これは台形の面積を表す.
![$\displaystyle \int_{a}^{b}x\,dx= \left[\frac{x^2}{2}\right]_{a}^{b}= \frac{b^2}{2}-\frac{a^2}{2}= \frac{1}{2}(b^2-a^2)= \frac{1}{2}(b-a)(b+a)\,.$](img3280.png) |
これは台形の面積を表す.
例 6.93 (定積分の計算例)
![$\displaystyle \int_{0}^{1}x^5\,dx= \left[\frac{x^6}{6}\right]_{0}^{1}= \frac{1}{6}-\frac{0}{6}= \frac{1}{6}.$](img3281.png) |
例 6.94 (定積分の計算例)
![$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos x\,dx= \Big[\sin x\Big]_{0}^{\frac{\pi}{2}}= \sin\frac{\pi}{2}-\sin 0= 1-0=1\,.$](img3282.png) |
例 6.95 (定積分の計算例)
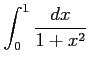 |
![$\displaystyle = \Big[\mathrm{Tan}^{-1} x\Big]_{0}^{1}= \mathrm{Tan}^{-1}(1)-\mathrm{Tan}^{-1}(0)= \frac{\pi}{4}-0=\frac{\pi}{4}\,.$](img3284.png) |
例 6.96 (定積分の計算例)
![$\displaystyle \int_{0}^{1} \frac{dx}{\sqrt{1+x^2}}= \left[\vrule height1.5em width0em depth0.1em\,{\sinh^{-1}(x)}\,\right]_{0}^{1}= \sinh^{-1}(1)-\sinh^{-1}(0)$](img3285.png) |
||
平成21年6月1日