6.20 定積分の置換積分
定理 6.97 (置換積分)
積分変数を 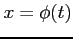 と置き換えると定積分は
と置き換えると定積分は
と表される.
 |
と表される.
例 6.98 (置換積分の計算例)
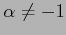 のとき,
のとき,
![$\displaystyle = \int_{0}^{1}(1-x)^{\alpha}\,dx= \left[\vrule height1.5em width0...
...(1-x)^{\alpha+1}}\,\right]_{0}^{1}= 0+\frac{1}{\alpha+1}= \frac{1}{\alpha+1}\,.$](img3289.png) |
例 6.99 (置換積分の計算例)
ここで,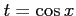 とおいて,
とおいて,
 ,
,
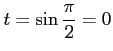 ,
,
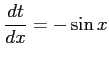 ,
,
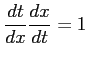 を用いた.
を用いた.
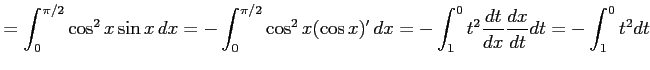 |
||
![$\displaystyle = \int_{0}^{1}t^2dt= \left[\vrule height1.5em width0em depth0.1em\,{\frac{t^3}{3}}\,\right]_{0}^{1}= \frac{1}{3}.$](img3291.png) |
ここで,
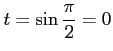 ,
,
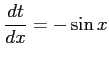 ,
,
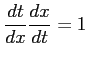 を用いた.
を用いた.
例 6.100 (置換積分の計算例)
ここで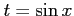 とおいた.このとき
とおいた.このとき
であることを用いた. また積分区間は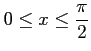 から
から
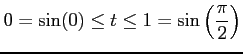 へと変わる.
へと変わる.
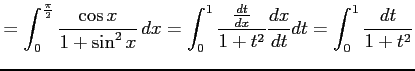 |
||
![$\displaystyle = \Big[\mathrm{Tan}^{-1} x\Big]_{0}^{1}= \mathrm{Tan}^{-1}(1)-\mathrm{Tan}^{-1}(0)= \frac{\pi}{4}-0=\frac{\pi}{4}\,.$](img3284.png) |
ここで
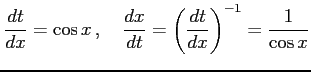 |
であることを用いた. また積分区間は
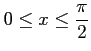 から
から
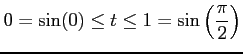 へと変わる.
へと変わる.
例 6.101 (置換積分の計算例)
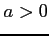 のき,
のき,
ここで,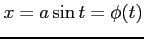 とおいて,
とおいて,
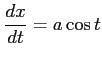 ,
,
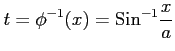 ,
,
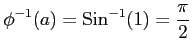 ,
,
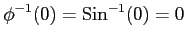 を用いた.
を用いた.
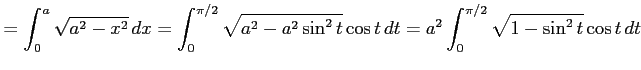 |
||
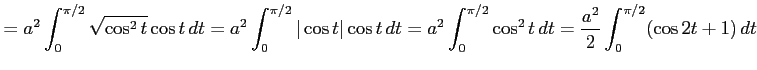 |
||
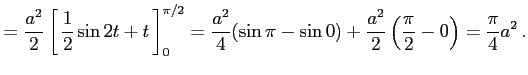 |
ここで,
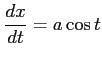 ,
,
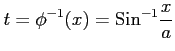 ,
,
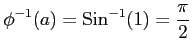 ,
,
例 6.102 (置換積分を用いた定積分)
ここで,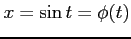 とおいて,
とおいて,
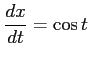 ,
,
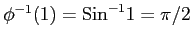 ,
,
 を用いた.
を用いた.
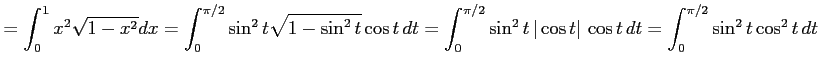 |
||
![$\displaystyle = \int_{0}^{\pi/2}(\sin t\cos t)^2\,dt= \int_{0}^{\pi/2}\left(\fr...
...ule height1.5em width0em depth0.1em\,{t-\frac{\sin 4t}{4}}\,\right]_{0}^{\pi/2}$](img3307.png) |
||
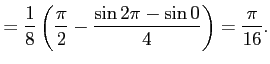 |
ここで,
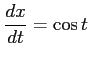 ,
,
例 6.103 (置換積分を用いた定積分)
ここで, とおいて,
とおいて,
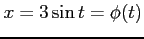 ,
,
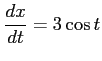 ,
,
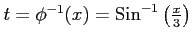 ,
,
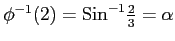 ,
,
 を用いた.
また,
を用いた.
また,
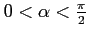 より,
より,
 (
(
![$ t\in[0,\alpha]$](img3322.png) ) であり,
) であり,
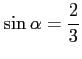 より,
より,
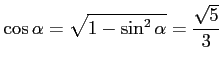 で
あることを用いた.
で
あることを用いた.
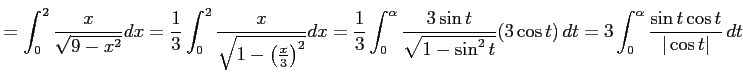 |
||
![$\displaystyle = 3 \int_{0}^{\alpha}\frac{\sin t\cos t}{\cos t}\,dt= 3 \int_{0}^...
...\right]_{0}^{\alpha}= -3\cos\alpha+3\cos 0= -3\frac{\sqrt{5}}{3}+3= 3-\sqrt{5}.$](img3314.png) |
ここで,
 とおいて,
とおいて,
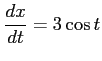 ,
,
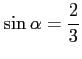 より,
より,
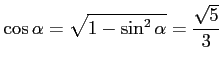 で
あることを用いた.
で
あることを用いた.
例 6.104 (置換積分を用いた定積分)
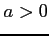 のとき,
のとき,
ここで,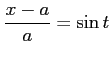 とおき,
とおき,
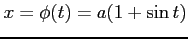 ,
,
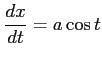 ,
,
 ,
,
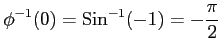 ,
,
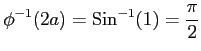 を用いた.
を用いた.
 |
||
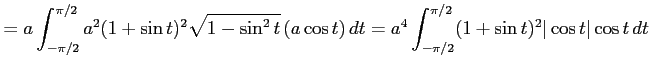 |
||
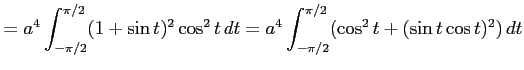 |
||
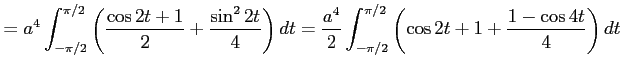 |
||
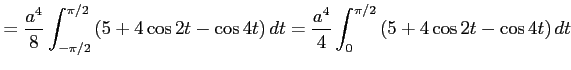 |
||
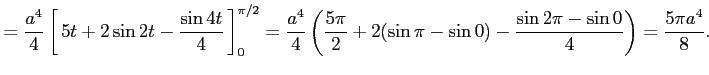 |
ここで,
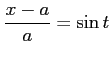 とおき,
とおき,
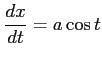 ,
,
 ,
,
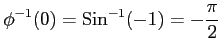 ,
,
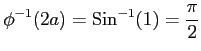 を用いた.
を用いた.
例 6.105 (双曲線関数を用いた定積分)
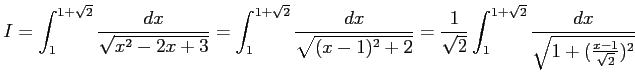 |
||
![$\displaystyle = \frac{\sqrt{2}}{\sqrt{2}} \int_{1}^{1+\sqrt{2}}\frac{(\frac{x-1...
...c{x-1}{\sqrt{2}}\right)}\,\right]_{1}^{1+\sqrt{2}}= \sinh^{-1}(1)-\sinh^{-1}(0)$](img3337.png) |
||
例 6.106 (双曲線関数を用いた定積分)
定積分
を考える. 積分区間が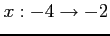 であるから
であるから 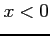 である.
このことに注意して変数変換を
である.
このことに注意して変数変換を
とする.このとき積分区間は
となる.また
であることを用いると
となる.ここで
であることを用いる.このとき
より
となる.また
である.よって
を得る.
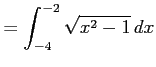 |
を考える. 積分区間が
とする.このとき積分区間は
となる.また
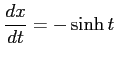 |
であることを用いると
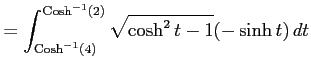 |
||
| (積分区間をひっくり返す.
|
||
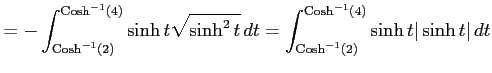 |
||
| (
|
||
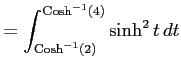 |
||
| (
|
||
![$\displaystyle = \frac{1}{2} \int^{\mathrm{Cosh}^{-1}(4)}_{\mathrm{Cosh}^{-1}(2)...
... \frac{1}{2}\sinh(2t)-t \right]^{\mathrm{Cosh}^{-1}(4)}_{\mathrm{Cosh}^{-1}(2)}$](img3351.png) |
||
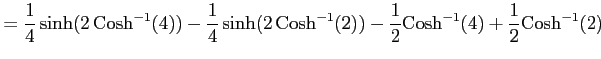 |
となる.ここで
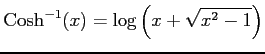 |
であることを用いる.このとき
 |
||
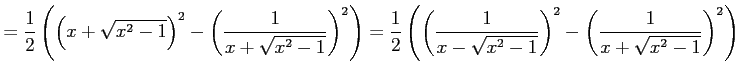 |
||
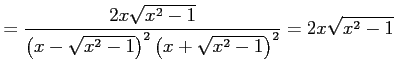 |
より
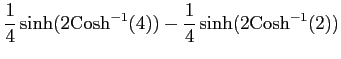 |
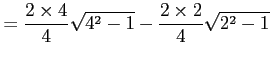 |
|
となる.また
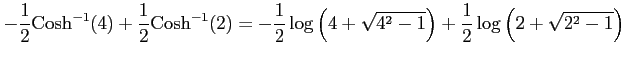 |
||
 |
である.よって
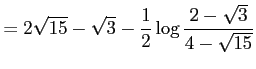 |
||
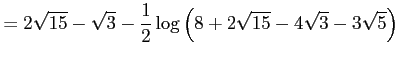 |
を得る.
例 6.107 (双曲線関数を用いた定積分)
定積分
を求める.
とおく.すると,
となる.ここで,
である.これらを代入すると
を得る.
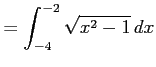 |
を求める.
とおく.すると,
![$\displaystyle = \frac{1}{4} \int_{\alpha}^{\beta}\left( t-\frac{2}{t}+\frac{1}{...
...ac{1}{4} \left[ \frac{t^2}{2}- 2\log t- \frac{1}{2t^2} \right]_{\alpha}^{\beta}$](img3365.png) |
||
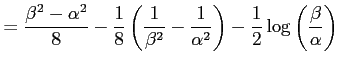 |
となる.ここで,
である.これらを代入すると
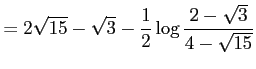 |
||
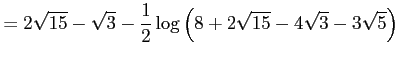 |
を得る.
平成21年6月1日