6.21 定積分の部分積分
定理 6.108 (部分積分)
![$\displaystyle \int_{a}^{b}f'(x)g(x)\,dx= \Big[f(x)g(x)\Big]_{a}^{b}- \int_{a}^{b}f(x)g'(x)\,dx\,.$](img3368.png) |
例 6.109 (部分積分の計算例)
![$\displaystyle = \int_{0}^{\pi}x\,\sin x\,dx= \int_{0}^{\pi}x\,(-\cos x)'\,dx= \Big[-x\cos x\Big]_{0}^{\pi}- \int_{0}^{\pi}1\times(-\cos x)\,dx$](img3369.png) |
||
![$\displaystyle = \Big[-x\cos x\Big]_{0}^{\pi}+ \int_{0}^{\pi}\cos x\,dx= \Big[-x...
...Big]_{0}^{\pi}+ \Big[\sin x\Big]_{0}^{\pi}= \Big[-x\cos x+\sin x\Big]_{0}^{\pi}$](img3370.png) |
||
例 6.110 (部分積分の計算例)
![$\displaystyle = \int_{0}^{1}xe^{2x}\,dx= \frac{1}{2}\int_{0}^{1}x(e^{2x})'\,dx=...
...em width0em depth0.1em\,{\frac{1}{2}xe^{2x}-\frac{1}{4}e^{2x}}\,\right]_{0}^{1}$](img3372.png) |
||
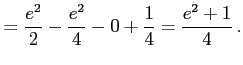 |
例 6.111 (部分積分の計算例)
ここで,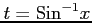 ,
,
 とおき,
とおき,
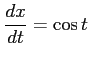 ,
,
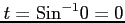 ,
,
 を用いた.
を用いた.
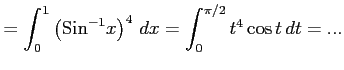 |
ここで,
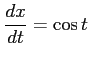 ,
,
 を用いた.
を用いた.
平成21年6月1日