6.22 偶関数と奇関数の定積分
定理 6.112 (偶関数,奇関数の定積分)
関数 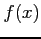 が偶関数のとき
が偶関数のとき
関数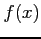 が奇関数のとき
が奇関数のとき
が成り立つ. 関数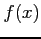 が奇関数のとき
が奇関数のとき
が成り立つ.
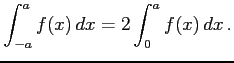 |
関数
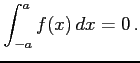 |
(証明)
関数 ![]() が偶関数のとき
が偶関数のとき
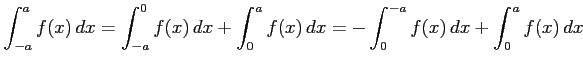 |
||
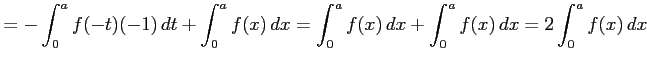 |
が成り立つ. 関数
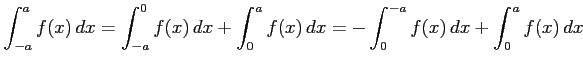 |
||
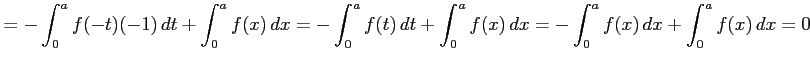 |
が成り立つ.
平成21年6月1日