6.23 三角関数の定積分
問 6.113 (三角関数の定積分)
自然数 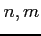 に対して
に対して
となることを示せ. ただし,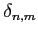 はクロネッカーのデルタ(Kronecker's
delta) である.
はクロネッカーのデルタ(Kronecker's
delta) である.
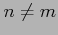 のとき,
のとき,
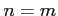 のとき,
のとき,
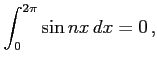 |
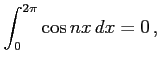 |
|||||
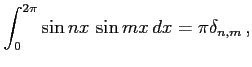 |
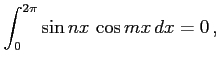 |
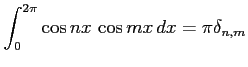 |
となることを示せ. ただし,
(答え)
![$\displaystyle \int_{0}^{2\pi}\cos nx\,dx= \left[\vrule height1.5em width0em dep...
...em\,{\frac{1}{n}\sin nx}\,\right]_{0}^{2\pi}= \frac{1}{n}(\sin 2n\pi-\sin 0)=0.$](img3391.png) |
||
![$\displaystyle \int_{0}^{2\pi}\sin nx\,dx= \left[\vrule height1.5em width0em dep...
... nx}\,\right]_{0}^{2\pi}= \frac{-1}{n}(\cos 2n\pi-\cos 0)= \frac{-1}{n}(1-1)=0.$](img3392.png) |
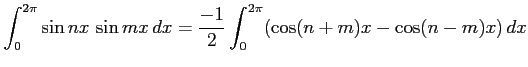 |
||
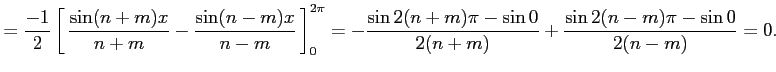 |
||
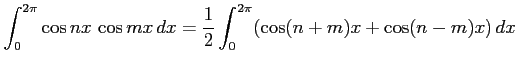 |
||
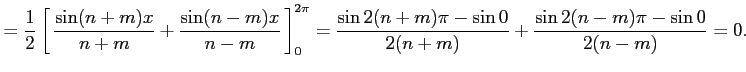 |
||
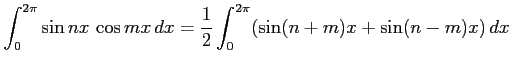 |
||
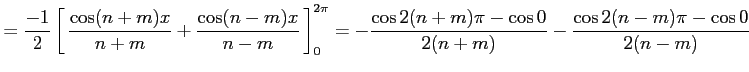 |
||
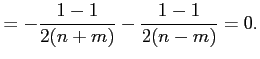 |
![$\displaystyle \int_{0}^{2\pi} \sin nx\,\sin nx\,dx= \int_{0}^{2\pi} \sin^2 nx\,...
...t1.5em width0em depth0.1em\,{\frac{x}{2}-\frac{\sin 2x}{4}}\,\right]_{0}^{2\pi}$](img3402.png) |
||
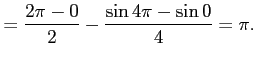 |
||
![$\displaystyle \int_{0}^{2\pi} \cos nx\,\cos nx\,dx= \int_{0}^{2\pi} \cos^2 nx\,...
...t1.5em width0em depth0.1em\,{\frac{\sin 2x}{4}+\frac{x}{2}}\,\right]_{0}^{2\pi}$](img3404.png) |
||
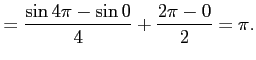 |
||
![$\displaystyle \int_{0}^{2\pi} \sin nx\,\cos nx\,dx= \frac{1}{2} \int_{0}^{2\pi}...
...cos 2x}{4}}\,\right]_{0}^{2\pi}= -\frac{\cos 4\pi-\cos 0}{4}= -\frac{1-1}{4}=0.$](img3406.png) |
平成21年6月1日
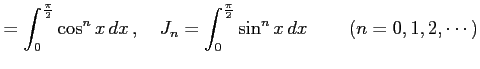
![$\displaystyle I_{n}=J_{n}= \frac{(n-1)!!}{n!!}\varepsilon_{n}\,,\qquad \varepsi...
...($n$: 偶数)} \\ [2ex] \displaystyle{1} & \text{($n$: 奇数)} \end{array} \right.$](img3408.png)
![[*]](crossref.png)