6.28 演習 〜 定積分
問 6.131 (定積分)
次を示せ.
(1)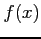 が偶関数のとき
が偶関数のとき
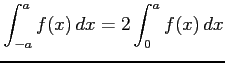
(2)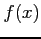 が奇関数のとき
が奇関数のとき
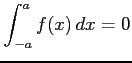
(1)
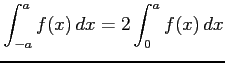
(2)
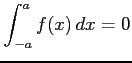
問 6.132 (定積分)
次の定積分を求めよ.
(1) (2)
(2)
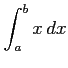 (3)
(3)
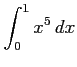 (4)
(4)
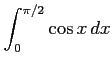 (5)
(5)
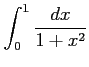 (6)
(6)
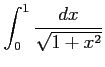
(7)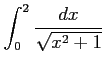
(1)
 (2)
(2)
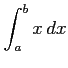 (3)
(3)
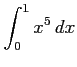 (4)
(4)
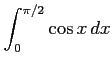 (5)
(5)
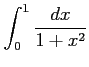 (6)
(6)
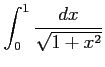
(7)
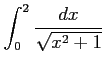
問 6.133 (定積分の置換積分)
次の定積分を求めよ.(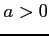 )
)
(1)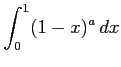 (2)
(2)
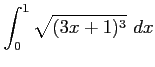 (3)
(3)
 (4)
(4)
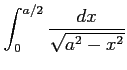
(5)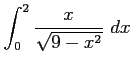 (6)
(6)
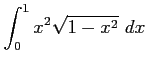 (7)
(7)
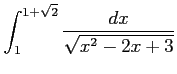 (8)
(8)
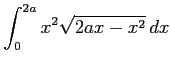
(9)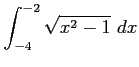 (10)
(10)
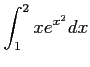 (11)
(11)
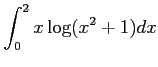 (12)
(12)
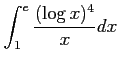
(1)
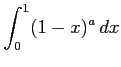 (2)
(2)
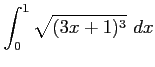 (3)
(3)
 (4)
(4)
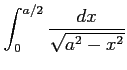
(5)
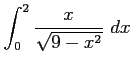 (6)
(6)
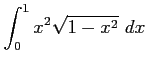 (7)
(7)
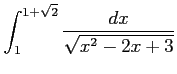 (8)
(8)
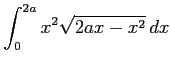
(9)
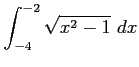 (10)
(10)
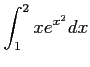 (11)
(11)
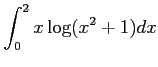 (12)
(12)
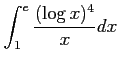
問 6.134 (定積分の部分積分)
次の定積分を求めよ.
(1)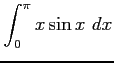 (2)
(2)
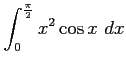 (3)
(3)
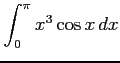 (4)
(4)
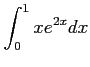 (5)
(5)

(6)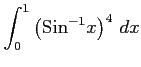 (
(
 )
)
(1)
 (2)
(2)
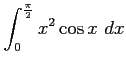 (3)
(3)
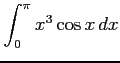 (4)
(4)
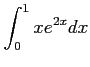 (5)
(5)

(6)
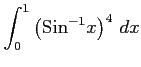 (
(
問 6.135 (有理式の定積分)
次の定積分を求めよ.
(1)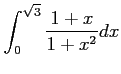 (2)
(2)
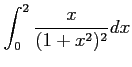 (3)
(3)
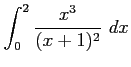 (4)
(4)
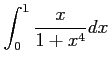
(1)
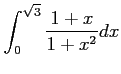 (2)
(2)
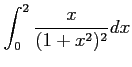 (3)
(3)
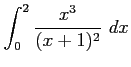 (4)
(4)
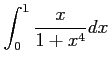
問 6.136 (三角関数の定積分)
次の定積分を求めよ.
(1) (2)
(2)
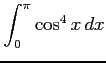 (3)
(3)
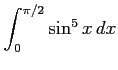 (4)
(4)
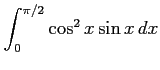
(5) (6)
(6)
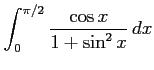 (7)
(7)
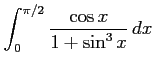
(1)
 (2)
(2)
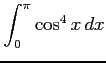 (3)
(3)
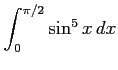 (4)
(4)
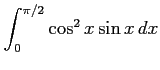
(5)
 (6)
(6)
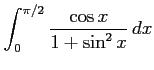 (7)
(7)
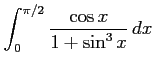
問 6.137 (三角関数の定積分)
自然数 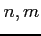 に対して次の定積分が成立することを示せ.
に対して次の定積分が成立することを示せ.
(1)
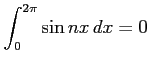 (2)
(2)
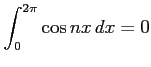 (3)
(3)

(4)
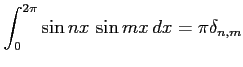 (5)
(5)
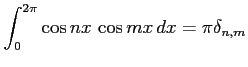
問 6.138 (定積分)
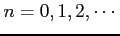 に対して
次の定積分が成立することを示せ.
に対して
次の定積分が成立することを示せ.
(1)
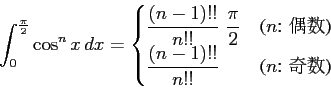 (2)
(2)
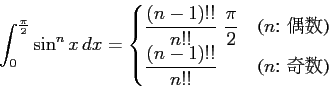
問 6.139 (面積)
次の領域の面積を定積分で求めよ.
(1) 単位円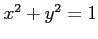 の内部の領域.
(2) 楕円
の内部の領域.
(2) 楕円
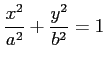
 の内部の領域
の内部の領域
(3) 曲線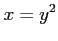 と直線
と直線 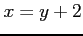 とで囲まれてできる領域.
とで囲まれてできる領域.
(4) 2 つの曲線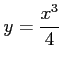 ,
, 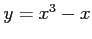 で囲まれてできる領域.
で囲まれてできる領域.
(5) 円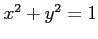 を直線
を直線  で 2 つに分割してできる上側の領域.
で 2 つに分割してできる上側の領域.
(6) 曲線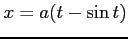 ,
,
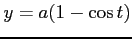 (
(
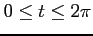 )
と
)
と 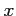 軸とで囲まれてできる領域.
軸とで囲まれてできる領域.
(7) 曲線 ,
,
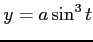 (
(
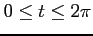 )
と
)
と 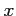 軸とで囲まれてできる領域.
軸とで囲まれてできる領域.
(8) 曲線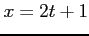 ,
, 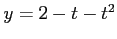 と
と  軸とで囲まれてできる領域.
軸とで囲まれてできる領域.
(9) 曲線 ,
, 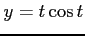 (
(
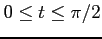 )
と
)
と 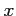 軸とで囲まれてできる領域.
軸とで囲まれてできる領域.
(10) 曲線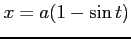 ,
,
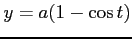 (
(
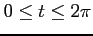 )
と
)
と 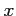 軸とで囲まれてできる領域.
軸とで囲まれてできる領域.
(1) 単位円
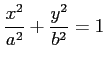
(3) 曲線
(4) 2 つの曲線
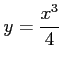 ,
, (5) 円
(6) 曲線
(7) 曲線
(8) 曲線
(9) 曲線
(10) 曲線
問 6.140 (曲線の長さ)
次の曲線の長さを定積分で求めよ.
(1) 単位円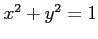 の円周の長さ.
(2)
の円周の長さ.
(2) 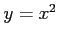 (
(
 )
)
(3)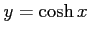 (
(
 )
(4)
)
(4)
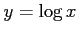 (
(
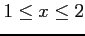 )
)
(5)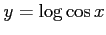 (
(
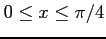 )
(6)
)
(6)
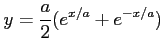 (
(
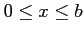 )
)
(7)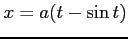 ,
,
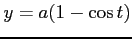 (
(
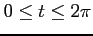 )
(8)
)
(8)
 ,
,
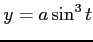 (
(
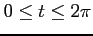 )
)
(9)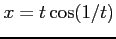 ,
,
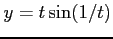 (
(
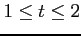 )
(10)
)
(10) 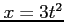 ,
, 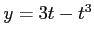 (
(
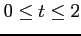 )
)
(1) 単位円
(3)
(5)
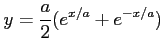 (
(
(7)
(9)
問 6.141 (回転体の体積)
次の体積を求めよ.
(1)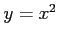 ,
, 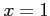 ,
, 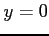 とで囲まれてできる領域を
とで囲まれてできる領域を
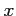 軸回りで 1 回転してできる立体.
軸回りで 1 回転してできる立体.
(2)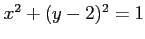 の内部の領域を
の内部の領域を 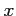 軸回りで 1 回転してできる立体.
軸回りで 1 回転してできる立体.
(1)
(2)
平成21年6月1日