6.29 広義積分
有限区間で連続な関数に対し定義される量が定積分である. 不連続点を含む区間や無限区間における積分へ拡張する. この拡張された積分を広義積分(improper integral)という.
定義 6.142 (不連続点を含む区間での広義積分)
関数 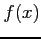 が
が 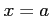 で不連続で,区間
で不連続で,区間 ![$ (a,b]$](img3575.png) で連続なとき,
で連続なとき,
 で不連続で,区間
で不連続で,区間 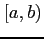 で連続なとき,
で連続なとき,
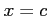
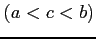 で不連続で,区間
で不連続で,区間 ![$ [a,b]$](img62.png) で連続なとき,
で連続なとき,
以上の極限が存在するとき広義積分は収束するという.
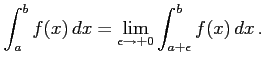 |
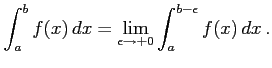 |
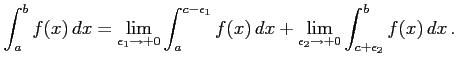 |
以上の極限が存在するとき広義積分は収束するという.
例 6.143 (不連続点を含む広義積分の具体例)
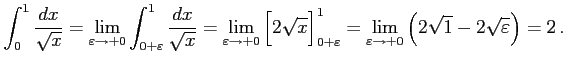 |
||
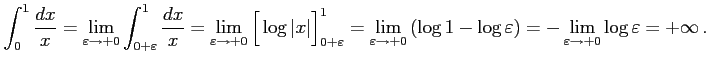 |
||
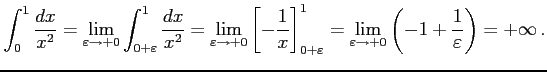 |
定理 6.144 (広義積分の収束次数)
実数 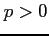 に対して次の広義積分が成り立つ:
に対して次の広義積分が成り立つ:
![$\displaystyle \int_{0}^{1}\frac{dx}{x^p}= \left\{\begin{array}{ll} \displaystyle{\frac{1}{1-p}} & (0<p<1) \\ [1em] +\infty & (p\geq1) \end{array}\right.$](img3585.png) |
問 6.145 (広義積分の収束次数)
これを示せ.
例 6.146 (広義積分の計算例)
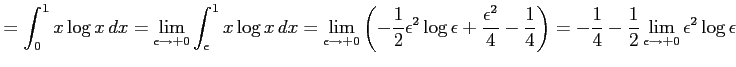 |
||
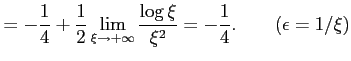 |
||
![$\displaystyle = \int_{\epsilon}^{1}x\log x\,dx= \frac{1}{2}\int_{\epsilon}^{1}(...
...ac{1}{2}x^2\log x}\,\right]_{\epsilon}^{1}- \frac{1}{2}\int_{\epsilon}^{1}x\,dx$](img3589.png) |
||
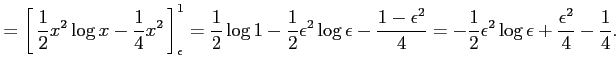 |
例 6.147 (広義積分の計算例)
ここで,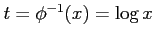 ,
,
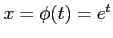 とおき,
とおき,
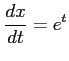 ,
,
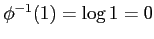 ,
,
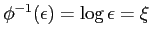 を用いた.
を用いた.
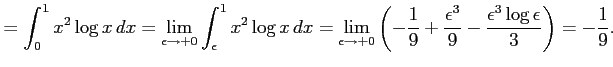 |
||
![$\displaystyle = \int_{\epsilon}^{1}x^2\log x\,dx= \int_{\xi}^{0}e^{2t}te^{t}\,d...
...m depth0.1em\,{te^{3t}}\,\right]_{\xi}^{0}- \frac{1}{3}\int_{\xi}^{0}e^{3t}\,dt$](img3592.png) |
||
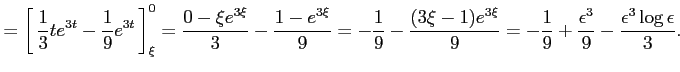 |
ここで,
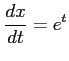 ,
,
定義 6.148 (無限区間での広義積分)
関数 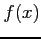 が無限区間
が無限区間
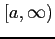 で連続なとき,
で連続なとき,
無限区間![$ (-\infty,b]$](img3601.png) で連続なとき,
で連続なとき,
無限区間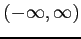 で連続なとき,
で連続なとき,
以上の極限が存在するとき広義積分は収束するという.
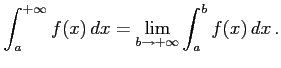 |
無限区間
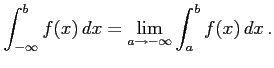 |
無限区間
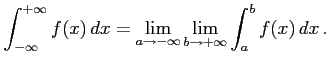 |
以上の極限が存在するとき広義積分は収束するという.
例 6.149 (無限区間での広義積分の具体例)
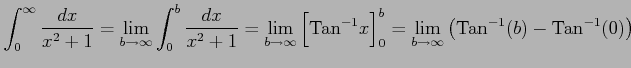 |
||
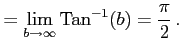 |
例 6.150 (無限区間での広義積分の具体例)
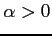 に対して
に対して
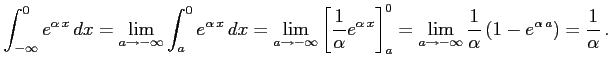 |
例 6.151 (無限区間での広義積分の具体例)
![$\displaystyle \int_{1}^{\infty}\frac{dx}{\sqrt{x}}= \lim_{b\to\infty} \int_{1}^...
...g[2\sqrt{x}\Big]_{1}^{b}= \lim_{b\to\infty} \left(2\sqrt{b}-2\right)=+\infty\,.$](img3609.png) |
||
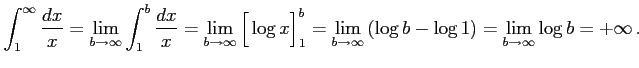 |
||
![$\displaystyle \int_{1}^{\infty}\frac{dx}{x^2}= \lim_{b\to\infty} \int_{1}^{b}\f...
...-\frac{1}{x}\right]_{1}^{b}= \lim_{b\to\infty} \left(-\frac{1}{b}+1\right)=1\,.$](img3611.png) |
定理 6.152 (広義積分の収束次数)
実数 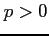 に対して次の広義積分が成り立つ:
に対して次の広義積分が成り立つ:
![$\displaystyle \int_{1}^{\infty}\frac{dx}{x^p}= \left\{\begin{array}{ll} +\infty & (0<p\leq1) \\ [1em] \displaystyle{\frac{1}{p-1}} & (p>1) \end{array}\right.$](img3612.png) |
問 6.153 (広義積分の収束次数)
これを示せ.
例 6.154 (広義積分の収束性)
広義積分
を考える.被積分関数は
の関係が成り立つので,
となる.ここで,
であるから,はさみうちの定理より,
を得る.
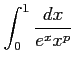 |
を考える.被積分関数は
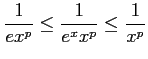 |
の関係が成り立つので,
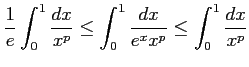 |
となる.ここで,
![$\displaystyle \int_{0}^{1}\frac{dx}{x^p}= \left\{\begin{array}{ll} \text{収束} & (0<p<1) \\ [1em] \text{発散} & (p\ge 1) \end{array}\right.$](img3616.png) |
であるから,はさみうちの定理より,
![$\displaystyle \int_{0}^{1} \frac{dx}{e^{x}x^{p}}= \left\{\begin{array}{ll} \text{収束} & (0<p<1) \\ [1em] \text{発散} & (p\ge 1) \end{array}\right.$](img3617.png) |
を得る.
平成21年6月1日