6.30 コーシーの主値積分
例 6.155 (極限は多価となる計算例)
広義積分では極限
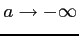 ,
,
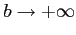 を独立に行う.
いま,
を独立に行う.
いま,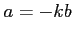 (
(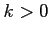 ) と条件を課して極限をとることにする.
つまり,定積分
) と条件を課して極限をとることにする.
つまり,定積分
において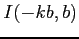 とおき,
とおき,
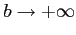 の極限をとる.
積分は
の極限をとる.
積分は
となる. (i) のとき積分は
のとき積分は 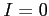 と有限確定する.
(ii)
と有限確定する.
(ii) 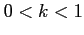 のとき積分は
のとき積分は 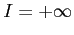 と無限確定する.
(iii)
と無限確定する.
(iii) 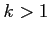 のとき積分は
のとき積分は 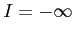 と無限確定する.
このように極限の取方により積分は様々な値をとる.
広義積分では極限の取り方によらず,値が一定のときのみ収束したとみなす.
この積分の場合は多価となるので,広義積分の意味では発散である.
と無限確定する.
このように極限の取方により積分は様々な値をとる.
広義積分では極限の取り方によらず,値が一定のときのみ収束したとみなす.
この積分の場合は多価となるので,広義積分の意味では発散である.
![$\displaystyle I(a,b)= \int_{a}^{b}x\,dx= \left[\vrule height1.5em width0em dept...
...em\,{\frac{x^2}{2}}\,\right]_{a}^{b}= \frac{b^2-a^2}{2} = \frac{1}{2}(b-a)(b+a)$](img3622.png) |
において
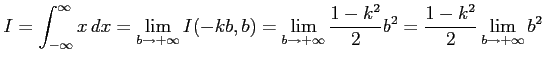 |
となる. (i)
定義 6.156 (コーシーの主値積分)
関数 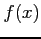 が
が 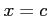
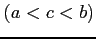 で不連続で,
有限区間
で不連続で,
有限区間 ![$ [a,b]$](img62.png) で連続なとき,
で連続なとき,
を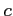 におけるコーシーの主値積分(Cauchy's principal values
of integral)という.
また関数
におけるコーシーの主値積分(Cauchy's principal values
of integral)という.
また関数 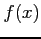 が無限区間
が無限区間
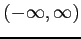 で連続なとき,
で連続なとき,
を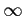 におけるコーシーの主値積分という.
主値積分はまた
におけるコーシーの主値積分という.
主値積分はまた
とも表記する.
v.p.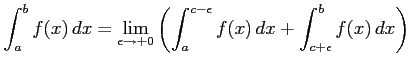 |
を
v.p.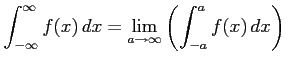 |
を
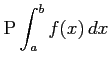 |
とも表記する.
例 6.157 (広義積分での計算例)
![$\displaystyle \int_{-\infty}^{\infty}x\,dx= \lim_{a\to-\infty}\lim_{b\to+\infty...
...2}{2}}\,\right]_{a}^{b}= \lim_{a\to-\infty}\lim_{b\to+\infty} \frac{b^2-a^2}{2}$](img3634.png) |
||
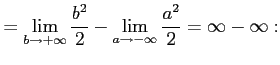 存在しない 存在しない |
例 6.158 (コーシーの主値積分での計算例)
v.p.![$\displaystyle \int_{-\infty}^{\infty}x\,dx= \lim_{a\to\infty} \int_{-a}^{a}x\,d...
....1em\,{\frac{x^2}{2}}\,\right]_{-a}^{a}= \lim_{a\to\infty} \frac{a^2-a^2}{2}=0.$](img3637.png) |
例 6.159 (広義積分での計算例)
![$\displaystyle \int_{-1}^{1}\frac{dx}{x}= \lim_{\varepsilon_{1}\to+0} \lim_{\var...
...}+ \lim_{\varepsilon_{2}\to+0} \Big[\log\vert x\vert\Big]_{\varepsilon_{2}}^{1}$](img3638.png) |
||
例 6.160 (コーシーの主値積分での計算例)
v.p.![$\displaystyle \int_{-1}^{1}\frac{dx}{x}= \lim_{\varepsilon\to+0} \left(\int_{-1...
...t x\vert\Big]_{-1}^{-\varepsilon}+ \Big[\log\vert x\vert\Big]_{\varepsilon}^{1}$](img3641.png) |
||
例 6.161 (広義積分での計算例)
![$\displaystyle \int_{-1}^{1}\frac{dx}{x^2}= \lim_{\varepsilon_{1}\to+0} \lim_{\v...
... height1.5em width0em depth0.1em\,{-\frac{1}{x}}\,\right]_{\varepsilon_{2}}^{1}$](img3643.png) |
||
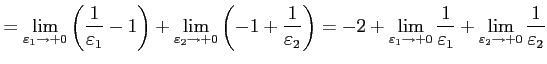 |
||
例 6.162 (コーシーの主値積分での計算例)
v.p.![$\displaystyle \int_{-1}^{1}\frac{dx}{x^2}= \lim_{\varepsilon\to+0} \left(\int_{...
...ight1.5em width0em depth0.1em\,{-\frac{1}{x}}\,\right]_{\varepsilon}^{1}\right)$](img3646.png) |
||
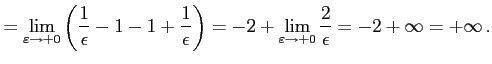 |
例 6.163 (広義積分での計算例)
![$\displaystyle \int_{-1}^{1}\frac{dx}{\sqrt{\vert x\vert}}= \lim_{\varepsilon_{1...
...ule height1.5em width0em depth0.1em\,{2\sqrt{x}}\,\right]_{\varepsilon_{2}}^{1}$](img3648.png) |
||
例 6.164 (コーシーの主値積分での計算例)
v.p.![$\displaystyle \int_{-1}^{1}\frac{dx}{\sqrt{\vert x\vert}}= \lim_{\varepsilon\to...
... height1.5em width0em depth0.1em\,{2\sqrt{x}}\,\right]_{\varepsilon}^{1}\right)$](img3651.png) |
||
例 6.165 (無限区間での広義積分の具体例)
![$\displaystyle \int_{-\infty}^{\infty} \frac{dx}{x^2+1}= \lim_{a\to-\infty} \lim...
...2+1}= \lim_{a\to-\infty} \lim_{b\to\infty} \Big[\mathrm{Tan}^{-1}x\Big]_{a}^{b}$](img3653.png) |
||
例 6.166 (コーシーの主値積分の計算例)
v.p.![$\displaystyle \int_{-\infty}^{\infty} \frac{dx}{1+x^2} = \lim_{a\to+\infty} \in...
...t[\vrule height1.5em width0em depth0.1em\,{\mathrm{Tan}^{-1}x}\,\right]_{0}^{a}$](img3655.png) |
||
平成21年6月1日