6.31 級数と定積分
例 6.167 (調和級数と定積分)
曲線
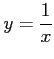 の面積を考える.
範囲が
の面積を考える.
範囲が
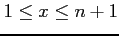 のときの面積を
のときの面積を 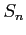 とする.
また,
幅が
とする.
また,
幅が 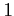 で高さが
で高さが
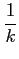 の
長方形の面積を
の
長方形の面積を
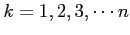 まで足合わせたものを
まで足合わせたものを 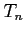 とする.
このときグラフを書けば明らかに
とする.
このときグラフを書けば明らかに
が成り立つ. よって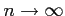 のとき
のとき
である.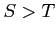 であるから,
調和級数
であるから,
調和級数 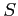 は発散する.
は発散する.
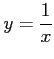 の面積を考える.
範囲が
の面積を考える.
範囲が
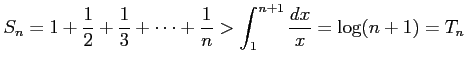 |
が成り立つ. よって
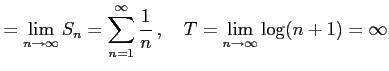 |
である.
例 6.168 (発散する級数と定積分)
である. よって級数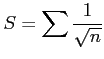 は発散する.
は発散する.
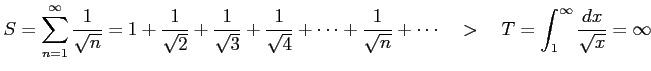 |
である. よって級数
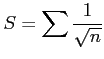 は発散する.
は発散する.
例 6.169 (収束する級数と定積分)
が成り立つ.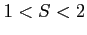 であるから
であるから
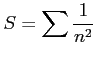 は収束する.
は収束する.
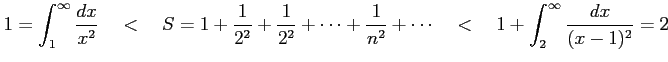 |
が成り立つ.
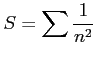 は収束する.
は収束する.
問 6.170 (級数の収束)
となることを示せ.
![$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^{p}} = \left\{ \begin{array}{cl} \text{発散} & (0<p\leq 1)\\ [1ex] \text{収束} & (p>1) \end{array} \right.$](img3669.png) |
となることを示せ.
平成21年6月1日