2.34 自然対数の底の公式を用いた極限の計算
公式 2.129 (ネピア数)
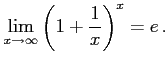 |
例 2.130 (関数の極限の計算例)
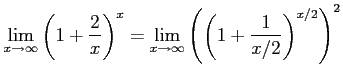 ( ( |
||
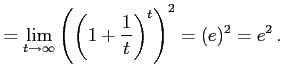 |
例 2.131 (関数の極限の計算例)
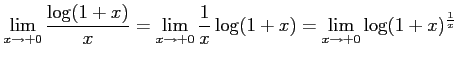 ( ( |
||
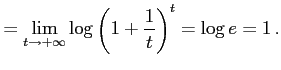 |
例 2.132 (関数の極限の計算例)
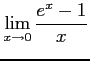 ( ( |
||
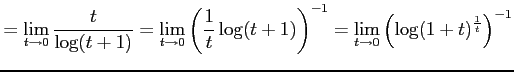 ( ( |
||
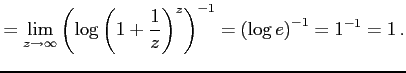 |
例 2.133 (関数の極限の計算例)
であるから,
を得る.
(証明)
![]() とおく.
さらに
とおく.
さらに
![]() とおくと,
とおくと,![]() と書ける.
このとき,
と書ける.
このとき,
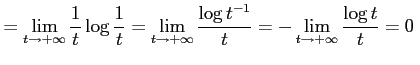 |
であるから,
を得る.
平成21年6月1日