3.6 負べきのべき関数の微分
定理 3.15 (負べき関数の微分)
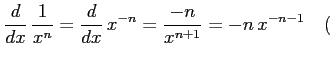 |
問 3.16
これを示せ.
となる.これを用いて
を得る.
(証明)
![]() とおく.
このとき
とおく.
このとき
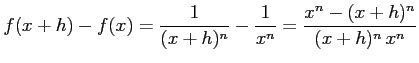 |
||
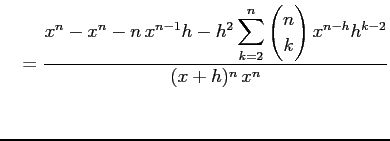 |
||
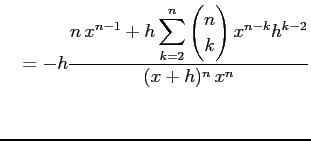 |
となる.これを用いて
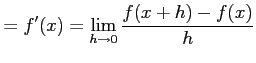 |
||
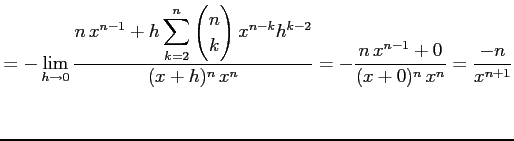 |
を得る.
平成21年6月1日
3.6 負べきのべき関数の微分
定理 3.15 (負べき関数の微分)
:自然数
問 3.16 これを示せ.
(証明)とおく. このとき
となる.これを用いて
を得る.
平成21年6月1日