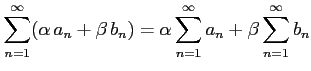4.15 収束するときにかぎり極限と四則演算は可換
例 4.48 (無限級数の結合則)
数列
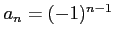 の
級数
の
級数
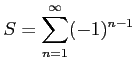 を考える.
すなわち
を考える.
すなわち
である. 足し算の順を入れ替えると
となる.また別の順で足し合わせると
となる. また,
の 2 式を足し合わせると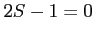 となり,
となり,
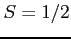 となる.
これらは矛盾する.
どこが誤りであろうか?
有限の項の和の常識は無限の項の和には通用しない.
この場合の間違いは足し算の順を変えたことである.
この例では結合則が成り立たない.
定義
となる.
これらは矛盾する.
どこが誤りであろうか?
有限の項の和の常識は無限の項の和には通用しない.
この場合の間違いは足し算の順を変えたことである.
この例では結合則が成り立たない.
定義 ![[*]](crossref.png) に従えば級数
に従えば級数 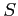 は発散である.
は発散である.
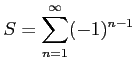 を考える.
すなわち
を考える.
すなわち
である. 足し算の順を入れ替えると
となる.また別の順で足し合わせると
となる. また,
の 2 式を足し合わせると
![[*]](crossref.png) に従えば級数
に従えば級数
問 4.49 (順番の入れ換え)
次の計算は誤りである.どこが間違っているか考えよ.
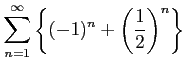 ( ( |
||
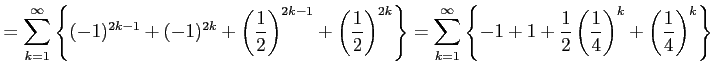 |
||
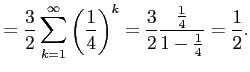 |
平成21年6月1日