4.14 級数
級数(series)とは数列 ![]() の和である.
式では
の和である.
式では
| (10) | ||
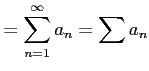 |
(11) |
と書き表す. 加法(足し算)は有限回の演算においてのみ定義されているので, 式(
![[*]](crossref.png) )は形式的な和である.
厳密に級数を定義するには次のように考える.
まず第
)は形式的な和である.
厳密に級数を定義するには次のように考える.
まず第 を考える. これを第
を考える. 数列
が存在したとする. このとき級数
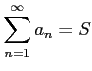 |
で与えられると定義する. 極限
定義 4.41 (級数)
数列 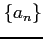 の和
の和
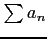 を級数(series)と呼び,
その値は
を級数(series)と呼び,
その値は
で定義する. この極限が存在するとき 級数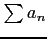 は収束する(convergent)といい,
収束しない場合を
級数
は収束する(convergent)といい,
収束しない場合を
級数
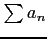 は発散する(divergent)という.
は発散する(divergent)という.
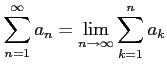 |
で定義する. この極限が存在するとき 級数
例 4.42 (調和級数)
級数
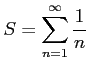 を考える.
部分和
を考える.
部分和
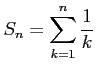 は
は
となる. 数列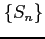 は発散する.
は発散する.
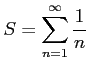 を考える.
部分和
を考える.
部分和
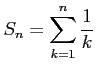 は
は
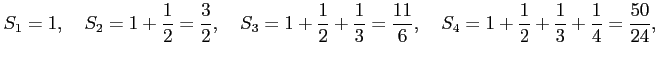 |
||
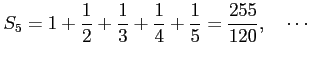 |
となる. 数列
例 4.43 (級数の計算)
級数
を考える.この部分和は
である. よって,級数は
と求まる.
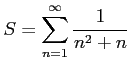 |
を考える.この部分和は
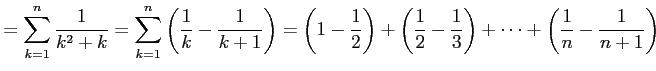 |
||
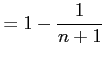 |
である. よって,級数は
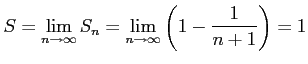 |
と求まる.
例 4.44 (級数の計算)
級数
を考える.この部分和は
である. よって,級数は
と求まる.
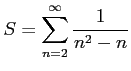 |
を考える.この部分和は
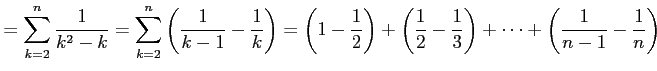 |
||
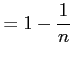 |
である. よって,級数は
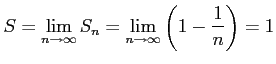 |
と求まる.
例 4.45 (級数の計算)
級数
を考える.この部分和は
である. よって,級数は
と求まる.
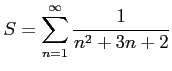 |
を考える.この部分和は
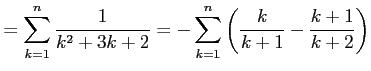 |
||
 |
である. よって,級数は
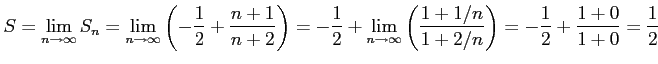 |
と求まる.
平成21年6月1日