2.10 ランダウの記号
定義 2.49 (ランダウの記号)
関数 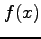 ,
, 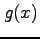 に対して
に対して
が成り立つとき,
と表記する.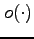 はランダウ(Landau)の記号である.
またこのとき,
はランダウ(Landau)の記号である.
またこのとき, 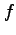 は
は 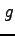 に比べ無視できるという.
に比べ無視できるという.
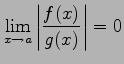 |
が成り立つとき,
と表記する.
定義 2.50 (ランダウの記号)
関数 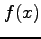 ,
, 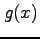 に対して
に対して
が成り立つとき,
と表記する.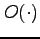 はランダウ(Landau)の記号である.
またこのとき
はランダウ(Landau)の記号である.
またこのとき 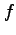 は
は 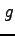 で押さえられるという.
で押さえられるという.
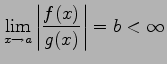 |
が成り立つとき,
と表記する.
注意 2.51 (二つのランダウの記号の関係)
関数 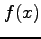 ,
, 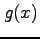 に対して
に対して
が成り立つとき,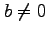 であれば
であれば
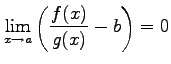 となるので
となるので
が成り立つ.
が成り立つとき,
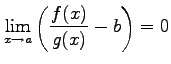 となるので
となるので
が成り立つ.
定義 2.52 (無限大,無限小)
関数 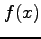 ,
, 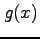 が
が 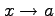 において無限小または
無限大となるとき,次の呼び方を定義する.
において無限小または
無限大となるとき,次の呼び方を定義する.
 ,
, 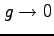 ,
, 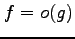
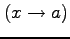 のとき,
のとき,
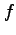 は
は 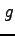 より高次の無限小と呼ぶ.
または
より高次の無限小と呼ぶ.
または 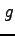 は
は 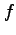 より低次の無限小と呼ぶ.
より低次の無限小と呼ぶ.
-
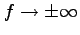 ,
,
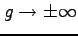 ,
, 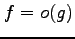
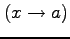 のとき,
のとき,
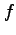 は
は 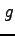 より低次の無限大と呼ぶ.
または
より低次の無限大と呼ぶ.
または 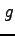 は
は 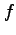 より高次の無限大と呼ぶ.
より高次の無限大と呼ぶ.
 ,
, 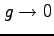 ,
, 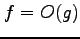
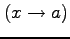 のとき,
のとき,
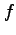 と
と 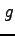 とは同次の無限小と呼ぶ.
とは同次の無限小と呼ぶ.
-
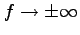 ,
,
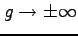 ,
, 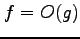
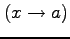 のとき,
のとき,
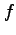 と
と 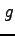 とは同次の無限大と呼ぶ.
とは同次の無限大と呼ぶ.
例 2.53 (ランダウの記号の使用例)
 の極限
の極限 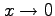 において,
において,
より
が成り立つ. よって,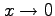 において
において  と
と  とは同次の無限小である.
また,
とは同次の無限小である.
また,
より,
が成り立つ. よって,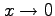 において
において 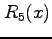 と
と 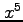 とは同次の無限小であり,
とは同次の無限小であり,
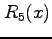 は
は 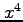 および
および 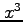 より高次の無限小である.
より高次の無限小である.
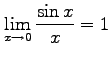 |
より
が成り立つ. よって,
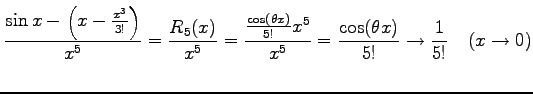 |
||
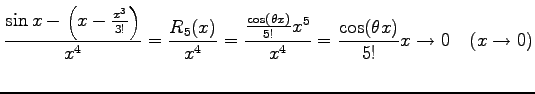 |
||
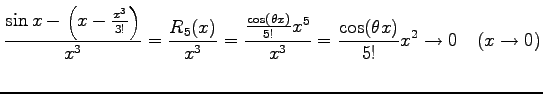 |
より,
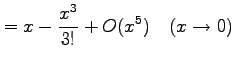 |
||
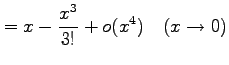 |
||
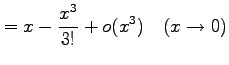 |
が成り立つ. よって,
例 2.54 (ランダウの記号の使用例)
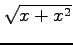 の極限
の極限
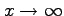 において,
において,
より
が成り立つ. よって,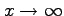 において
において
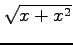 と
と  とは
同次の無限大である.
また,
とは
同次の無限大である.
また,
より
が成り立つ. よって,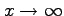 において
において
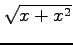 は
は 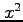 より
低次の無限大である.
より
低次の無限大である.
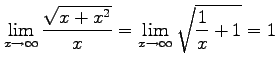 |
より
が成り立つ. よって,
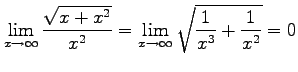 |
より
が成り立つ. よって,
注意 2.55 (テイラー展開とランダウの記号)
テイラー展開により
が成り立つ.なぜなら
となるからである.同様に
となることより得られる.
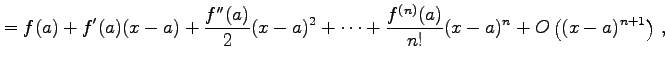 |
||
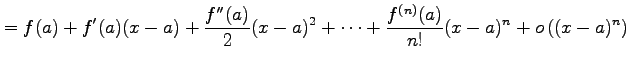 |
が成り立つ.なぜなら
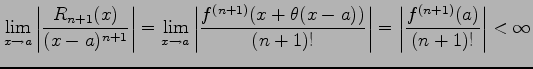 |
となるからである.同様に
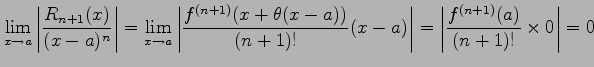 |
となることより得られる.
例 2.56 (ランダウの記号の使用例)
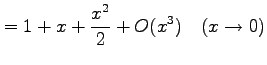 |
||
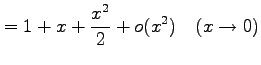 |
例 2.57 (ランダウの記号の使用例)
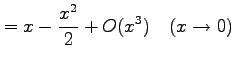 |
||
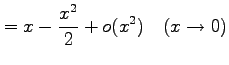 |
||
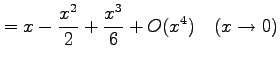 |
||
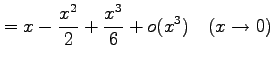 |
平成21年1月14日