2.19 2 変数関数 と 1 変数関数の合成関数の微分
定理 2.82 (合成関数の微分)
全微分可能な 2 変数関数 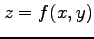 と
1 変数関数
と
1 変数関数 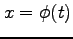 ,
, 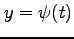 との
合成関数
との
合成関数
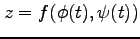 の導関数は
の導関数は
となる.また,代入も含めて正確に書くと
となる.
が成り立つ.または,
と表される. ただし,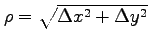 とおく.
このとき,
とおく.
このとき,
が成り立つ.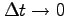 の極限をとると,
の極限をとると,
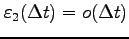 ,
,
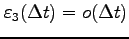 ,
,
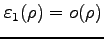 より,
より,
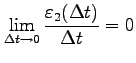 ,
,
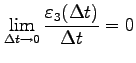 であり,
であり,
となるので,
を得る.
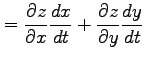 |
となる.また,代入も含めて正確に書くと
 |
となる.
(証明)
関数 ![]() は全微分可能であり,
関数
は全微分可能であり,
関数 ![]() ,
, ![]() は微分可能とする.
このとき
は微分可能とする.
このとき
が成り立つ.または,
と表される. ただし,
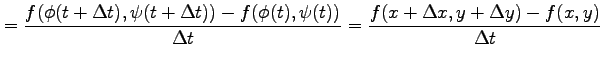 |
||
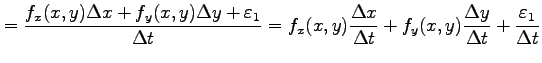 |
||
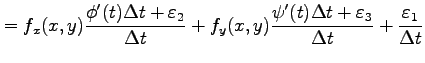 |
||
 |
が成り立つ.
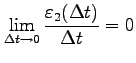 ,
,
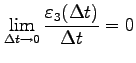 であり,
であり,
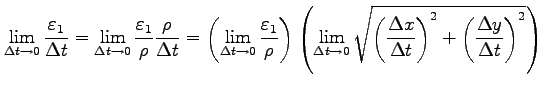 |
||
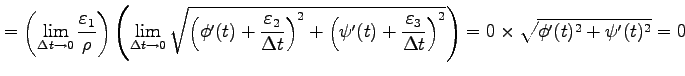 |
となるので,
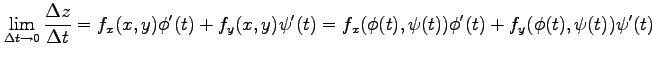 |
を得る.
例 2.83 (合成関数の微分)
関数 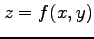 ,
, 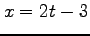 ,
, 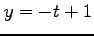 の合成関数
の合成関数
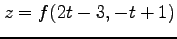 の導関数は,
の導関数は,
より
となる.
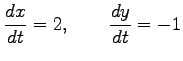 |
より
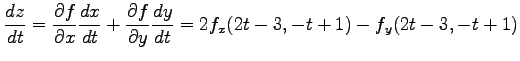 |
となる.
例 2.84 (合成関数の微分)
関数
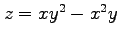 ,
, 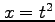 ,
, 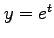 の
合成関数の導関数は,
の
合成関数の導関数は,
より
となる.
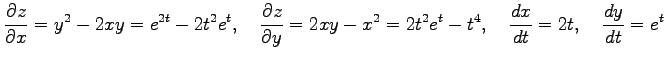 |
より
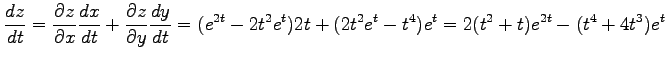 |
となる.
例 2.85 (合成関数の微分)
関数 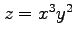 ,
, 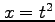 ,
, 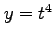 の合成関数の微分は,
の合成関数の微分は,
より
となる.
より
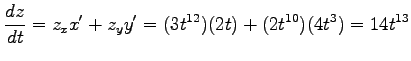 |
となる.
例 2.86 (合成関数の微分)
関数 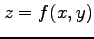 において,
合成関数
において,
合成関数
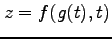 の
の
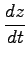 を求める.
を求める.
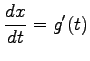 ,
,
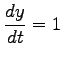 より
より
となる. さらにこの式の両辺を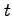 微分して
微分して
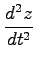 も求める.
上式の結果と第 1 項目の積の微分に注意して計算すると,
も求める.
上式の結果と第 1 項目の積の微分に注意して計算すると,
を得る.
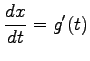 ,
,
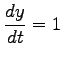 より
より
 |
となる. さらにこの式の両辺を
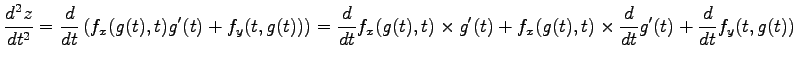 |
||
を得る.
例 2.87 (合成関数の微分)
関数 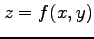 ,
, 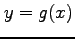 の
合成関数
の
合成関数
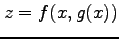 の
の  微分を考える.
まず,
微分を考える.
まず,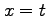 ,
, 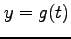 と置き換えて,
と置き換えて,
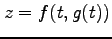 を
を 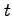 で微分する.
で微分する.
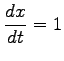 ,
,
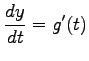 より
より
となる.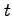 を
を  に置き換えると
に置き換えると
を得る. 同様にして,
を得る.
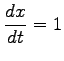 ,
,
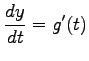 より
より
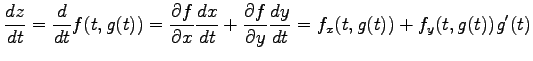 |
となる.
 |
を得る. 同様にして,
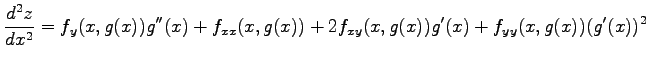 |
を得る.
例 2.88 (合成関数の微分)
関数 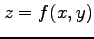 を用いて関数
を用いて関数
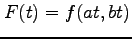 を考える.
このとき
を考える.
このとき 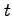 で微分すると
で微分すると
となる.さらに微分して
となる.
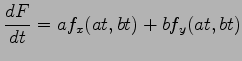 |
となる.さらに微分して
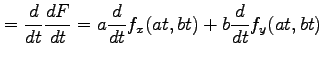 |
||
となる.
例 2.89 (合成関数の微分)
関数
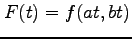 の 3 階導関数は
の 3 階導関数は
となる.
となる.
例 2.90 (合成関数の微分)
 ,
, 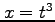 ,
, 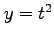 のとき,
のとき,
となる.
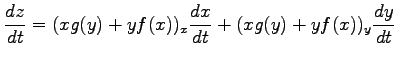 |
||
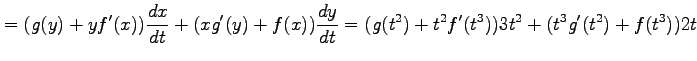 |
||
となる.
平成21年1月14日