2.18 1 変数関数の合成関数の微分
定理 2.81 (合成関数の微分)
関数 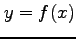 ,
, 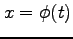 の合成関数
の合成関数
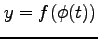 は
は
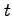 についての 1 変数関数であり,この合成関数の導関数は
についての 1 変数関数であり,この合成関数の導関数は
となる.または,代入も含めて正確に書くと
となる.
であり,
と表される.このとき,
となる. ここで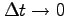 の極限をとると(●)が成り立つ.
このとき,
の極限をとると(●)が成り立つ.
このとき,
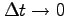 ,
,
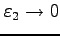 より,
(★)は
より,
(★)は
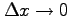 となる.
となる.
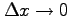 のとき(○)が成り立つ.
よって,(○), (●)より,
のとき(○)が成り立つ.
よって,(○), (●)より,
を得る.
 |
となる.または,代入も含めて正確に書くと
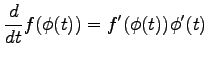 |
となる.
(証明)
関数 ![]() ,
, ![]() を微分可能とすると
を微分可能とすると
であり,
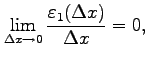 |
||
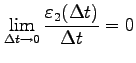 |
と表される.このとき,
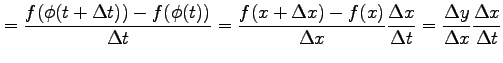 |
||
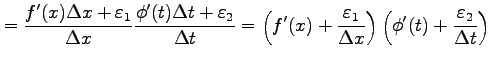 |
||
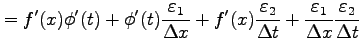 |
となる. ここで
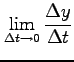 |
を得る.
平成21年1月14日