2.41 陰関数の高階導関数
例 2.181 (陰関数の高階偏導関数)
条件 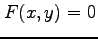 で定まる陰関数
で定まる陰関数 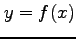 の高階導関数を求める.
条件
の高階導関数を求める.
条件 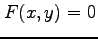 の両辺を
の両辺を  で微分すると
で微分すると
となる.さらに微分すると
となるので,
を得る.同様にして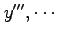 を求める.
を求める.
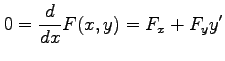 |
となる.さらに微分すると
| 0 | 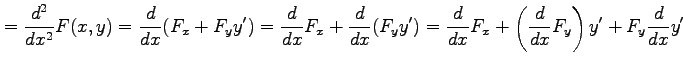 |
|
となるので,
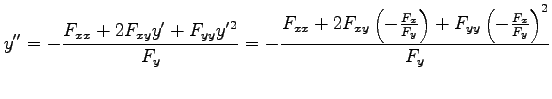 |
||
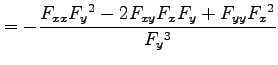 |
を得る.同様にして
例 2.182 (陰関数の高階偏導関数)
条件
 で定まる陰関数
で定まる陰関数 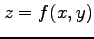 の高階偏導関数を求める.
条件
の高階偏導関数を求める.
条件
 の両辺を
の両辺を  と
と 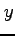 で偏微分すると
それぞれ
で偏微分すると
それぞれ
となる. 第 1 式をさらに で偏微分すると
で偏微分すると
となるので,
を得る. 第 1 式をさらに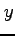 で偏微分すると
で偏微分すると
となるので,
を得る. 第 2 式をさらに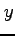 で偏微分すると
で偏微分すると
となるので,
を得る. 同様にして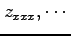 を求める.
を求める.
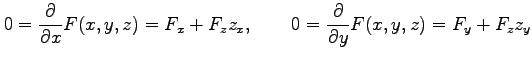 |
となる. 第 1 式をさらに
| 0 |  |
|
となるので,
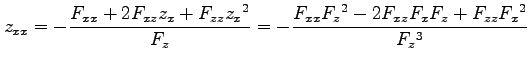 |
を得る. 第 1 式をさらに
| 0 |  |
|
となるので,
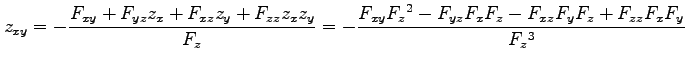 |
を得る. 第 2 式をさらに
| 0 | 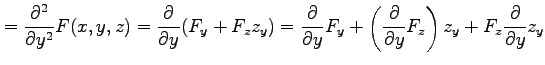 |
|
となるので,
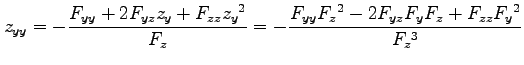 |
を得る. 同様にして
平成21年1月14日