2.43 演習問題 〜 陰関数,接線,接平面
問 2.190 (陰関数)
次の条件から定まる陰関数 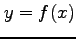 について
について
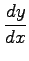 を求めよ.
を求めよ.
(1)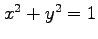 (2)
(2)
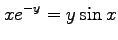 (3)
(3)
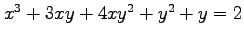
(4)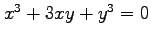 (5)
(5)
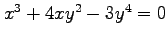 (6)
(6)
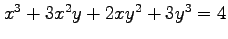
(7)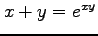 (8)
(8)
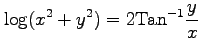 (9)
(9)
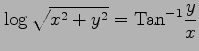
(10)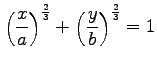 (
( )
(11)
)
(11)
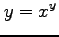
(1)
(4)
(7)
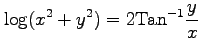 (9)
(9)
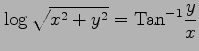
(10)
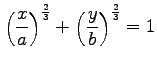 (
(
問 2.191 (陰関数)
次の条件から定まる陰関数 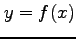 について
について
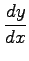 ,
,
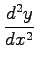 を求めよ.
を求めよ.
(1)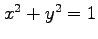 (2)
(2)
 (3)
(3)
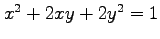 (4)
(4)
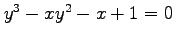
(5)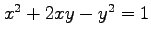
(1)
(5)
問 2.192 (陰関数の高階導関数)
条件 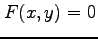 で定まる陰関数
で定まる陰関数 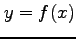 の導関数を求めよ.
の導関数を求めよ.
(1)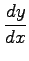 (2)
(2)
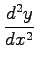
(1)
問 2.193 (陰関数の接線とテイラー展開)
次の曲線 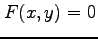 とその曲線上の点
とその曲線上の点 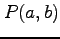 を考える.
条件
を考える.
条件 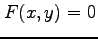 から定まる陰関数
から定まる陰関数 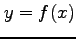 を
を
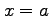 のまわりで
のまわりで  についてテイラー展開せよ.
についてテイラー展開せよ.
(1)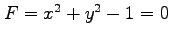 ,
,
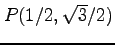 (2)
(2)
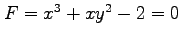 ,
, 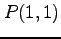
(3)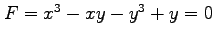 ,
, 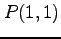 (4)
(4)
 ,
, 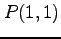
(5)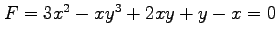 ,
, 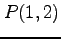 (6)
(6)
 ,
, 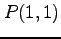
(7)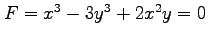 ,
, 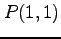
(1)
(3)
(5)
(7)
問 2.194 (接線)
次の曲線の点  における接線の方程式を求めよ.
における接線の方程式を求めよ.
(1)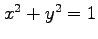 ,
,
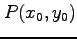 (2)
(2)
 ,
, 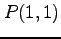
(3)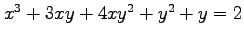 ,
, 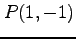 (4)
(4)
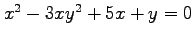 ,
, 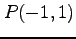
(5)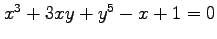 ,
, 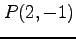 (6)
(6)
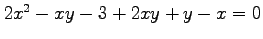 ,
, 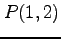
(7)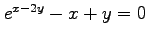 ,
, 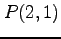 (8)
(8)
 ,
, 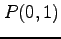
(9)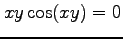 ,
,
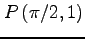 (10)
(10)
 ,
,
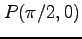
(1)
(3)
(5)
(7)
(9)
問 2.195 (陰関数)
次の条件から定まる陰関数 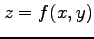 について
について
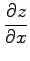 ,
,
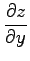 を求めよ.
を求めよ.
(1)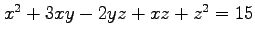 (2)
(2)
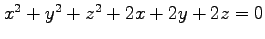
(3)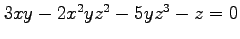 (4)
(4)
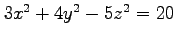
(5) (6)
(6)
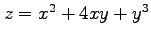 (7)
(7)
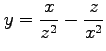 (8)
(8)
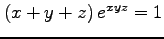
(9)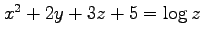 (10)
(10)
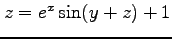 (11)
(11)
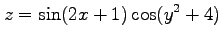
(12)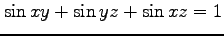 (13)
(13)
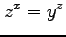
(1)
(3)
(5)
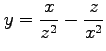 (8)
(8)
(9)
(12)
問 2.196 (陰関数)
次の条件から定まる陰関数 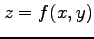 について
について
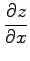 ,
,
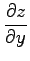 ,
,
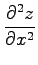 ,
,
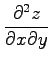 ,
,
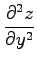 を求めよ.
を求めよ.
(1)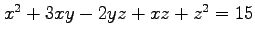 (2)
(2)
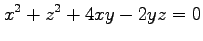 (3)
(3) 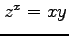
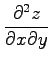 ,
,
(1)
問 2.197 (陰関数の高階導関数)
条件
 で定まる陰関数
で定まる陰関数 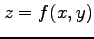 の偏導関数を求めよ.
の偏導関数を求めよ.
(1)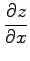 (2)
(2)
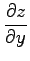 (3)
(3)
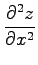 (4)
(4)
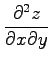 (5)
(5)
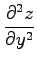
(1)
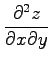 (5)
(5)
問 2.198 (陰関数の接平面とテイラー展開)
次の曲面
 とその曲面上の点
とその曲面上の点 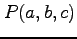 を考える.
条件
を考える.
条件
 で定まる陰関数
で定まる陰関数 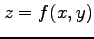 を
点
を
点 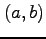 のまわりで点
のまわりで点 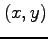 について
テイラー展開せよ.
について
テイラー展開せよ.
(1)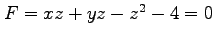 ,
, 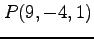 (2)
(2)
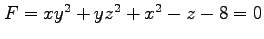 ,
, 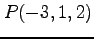
(1)
問 2.199 (接平面)
次の曲面の点  における接平面の方程式を求めよ.
における接平面の方程式を求めよ.
(1)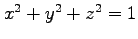 ,
,
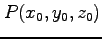 (2)
(2)
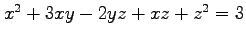 ,
,
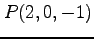
(3)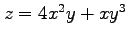 ,
,
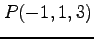 (4)
(4)
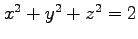 ,
,
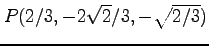
(5)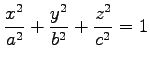 ,
,
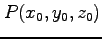 (6)
(6)
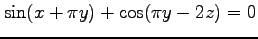 ,
,
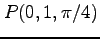
(7)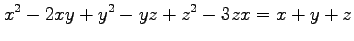 ,
,
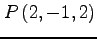
(1)
(3)
(5)
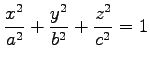 ,
,
(7)
平成21年1月14日