2.47 陰関数の極値問題
例 2.222 (陰関数の極値)
条件
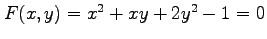 で定まる
陰関数
で定まる
陰関数 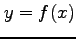 の極値を求める.
の極値を求める.
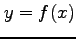 の導関数は
の導関数は
である. ただし,導関数が存在するのは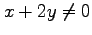 のときである.
のときである.
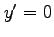 をみたす
をみたす 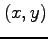 を求める.
を求める.
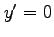 より,
より,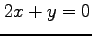 である.
これを変形して
である.
これを変形して 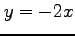 を
を 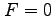 へ代入すると,
へ代入すると,
である. より,
極値の候補は
より,
極値の候補は
である. を求める.
を求める.
の両辺を微分すると,
より,
となる.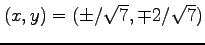 (復号同順)
のときの
(復号同順)
のときの  の値を求める.
の値を求める.
となるので, は極小値,
は極小値,
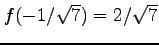 は極大値である.
は極大値である.
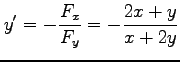 |
である. ただし,導関数が存在するのは
である.
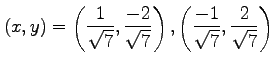 |
である.
の両辺を微分すると,
より,
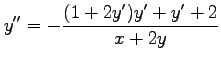 |
となる.
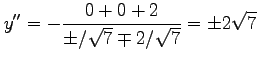 |
となるので,
平成21年1月14日