3.10 極座標への置換積分
例 3.51 (多重積分の変数変換)
多重積分
を求める. 積分変数を
とおく. このとき極座標への座標変換のヤコビアンは
であり,領域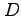 を
を
 で表すと,
で表すと,
となる. これらより,
を得る.
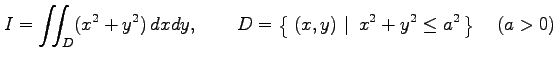 |
を求める. 積分変数を
とおく. このとき極座標への座標変換のヤコビアンは
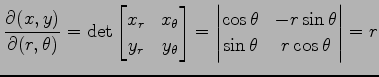 |
であり,領域
となる. これらより,
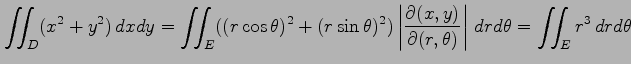 |
||
![$\displaystyle = \int_{0}^{2\pi}d\theta\int_{0}^{a}r^3\,dr= \left(\int_{0}^{2\pi...
...ht1.5em width0em depth0.1em\,{\frac{r^4}{4}}\,\right]_{0}^{a}=\frac{\pi a^4}{2}$](img2213.png) |
を得る.
注意 3.52 (極座標の面素)
直交座標 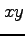 から極座標
から極座標 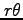 への変換で,
面素は
への変換で,
面素は
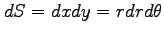 と変換される.
と変換される.
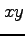 座標では辺の長さが
座標では辺の長さが 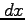 と
と 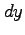 の長方形の面積であり,
の長方形の面積であり,
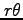 座標では辺の長さが
座標では辺の長さが 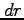 と
と
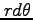 (半径
(半径 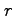 ,角
,角 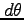 の円弧の長さ)の
長方形の面積となる.
の円弧の長さ)の
長方形の面積となる.
問 3.53 (多重積分の変数変換)
領域 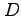 を
を  に関して単純な領域とみなし,
多重積分を
に関して単純な領域とみなし,
多重積分を
により求めよ.
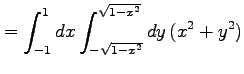 |
により求めよ.
![\includegraphics[width=0.35\textwidth]{chikan-polar2-D.eps}](img2219.png) |
![\includegraphics[width=0.35\textwidth]{chikan-polar2-rtheta.eps}](img2220.png) |
![\includegraphics[width=0.35\textwidth]{chikan-polar2-E.eps}](img2221.png) |
| (a) 領域 |
(b) |
(c) 領域 |
![\includegraphics[width=0.45\textwidth]{chikan-polar2-I.eps}](img2222.png) |
![\includegraphics[width=0.5\textwidth]{chikan-polar2-Ir.eps}](img2223.png) |
| (d) |
(e) |
平成21年1月14日