3.11 3 次元極座標への置換積分
例 3.54 (多重積分の変数変換)
多重積分
を求める. 積分変数を
とおく. このとき極座標への座標変換のヤコビアンは
であるから,体積素は
と表される. 領域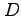 を
を
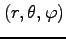 で表すと,
で表すと,
となる. これらより,
を得る.
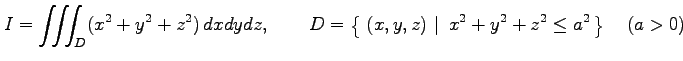 |
を求める. 積分変数を
とおく. このとき極座標への座標変換のヤコビアンは
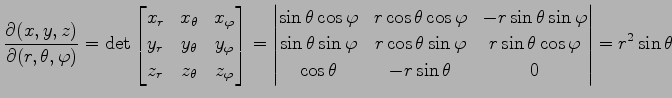 |
であるから,体積素は
と表される. 領域
となる. これらより,
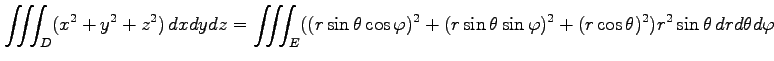 |
||
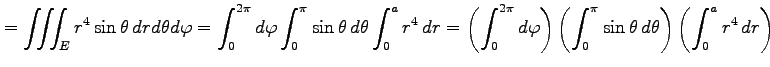 |
||
![$\displaystyle = \left[\vrule height1.5em width0em depth0.1em\,{\varphi}\,\right...
...1.5em width0em depth0.1em\,{\frac{r^5}{5}}\,\right]_{0}^{a}= \frac{4\pi a^5}{5}$](img2231.png) |
を得る.
問 3.55 (多重積分の変数変換)
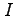 を次の累次積分を計算して求めよ.
を次の累次積分を計算して求めよ.
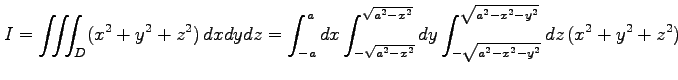 |
![\includegraphics[width=0.35\textwidth]{chikan-polar3-D.eps}](img2233.png) |
![\includegraphics[width=0.35\textwidth]{polar3.eps}](img2234.png) |
![\includegraphics[width=0.35\textwidth]{chikan-polar3-E.eps}](img2235.png) |
| (a) 領域 |
(b) 極座標 | (c) 領域 |
例 3.56 (多重積分の変数変換)
3 重積分
を求める. 3 次元の極座標に置き換えると 領域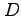 は
は
となる. 積分は
と求まる.
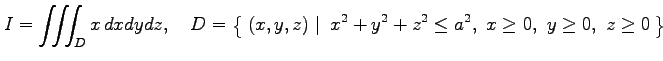 |
を求める. 3 次元の極座標に置き換えると 領域
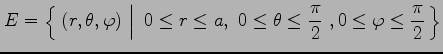 |
となる. 積分は
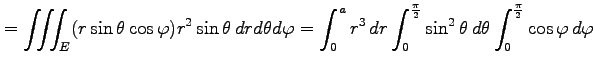 |
||
![$\displaystyle = \left[\vrule height1.5em width0em depth0.1em\,{\frac{r^4}{4}}\,...
...dth0em depth0.1em\,{\sin\varphi}\,\right]_0^{\frac{\pi}{2}} = \frac{\pi}{16}a^4$](img2238.png) |
と求まる.
例 3.57 (多重積分の変数変換)
多重積分
を計算する. ここで, 2 次元の極座標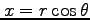 ,
,
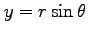 を用いると,
領域
を用いると,
領域  は
は
 座標では領域
座標では領域
となる. 多重積分を置換積分し, に関して単純な領域であることに注意して計算すると,
に関して単純な領域であることに注意して計算すると,
となる. ここで,
を用いると,
と求まる.![\includegraphics[width=0.4\textwidth]{taiseki-kyu-enchu-theta.eps}](img2246.png)
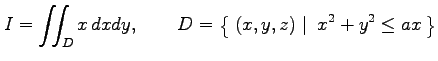 |
を計算する. ここで, 2 次元の極座標
 |
となる. 多重積分を置換積分し,
![$\displaystyle = \iiint_{E}r\cos\theta\,\, r\,drd\theta= \int_{-\pi/2}^{\pi/2}\c...
...height1.5em width0em depth0.1em\,{\frac{r^3}{3}}\,\right]_{r=0}^{r=a\cos\theta}$](img2241.png) |
||
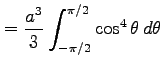 |
となる. ここで,
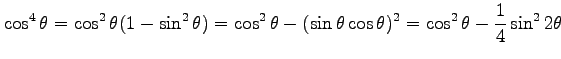 |
||
 |
を用いると,
![$\displaystyle = \frac{a^3}{3} \left[\vrule height1.5em width0em depth0.1em\,{\f...
...in2\theta+ \frac{1}{32}\sin4\theta}\,\right]_{-\pi/2}^{\pi/2}= \frac{\pi}{8}a^3$](img2245.png) |
と求まる.
![\includegraphics[width=0.4\textwidth]{taiseki-kyu-enchu-theta.eps}](img2246.png)
例 3.58 (多重積分の変数変換)
多重積分
を計算する. 領域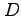 は
は
と書けるので, 中心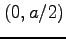 で半径
で半径 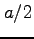 の円の内部の領域である.
ここで,
座標変換
の円の内部の領域である.
ここで,
座標変換
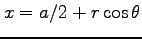 ,
,
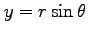 を考える.
このとき,領域
を考える.
このとき,領域 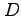 は
は
 座標で,
座標で,
となる.ヤコビアンは
となる. 多重積分を置換積分すると,
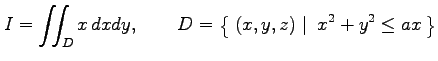 |
を計算する. 領域
と書けるので, 中心
となる.ヤコビアンは
 |
となる. 多重積分を置換積分すると,
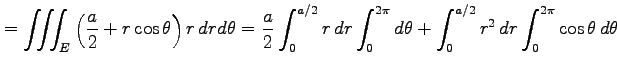 |
||
![$\displaystyle = \frac{a}{2} \left[\vrule height1.5em width0em depth0.1em\,{\fra...
....1em\,{\sin\theta}\,\right]_{0}^{2\pi} = \frac{\pi a^3}{8}+0 = \frac{\pi}{8}a^3$](img2254.png) |
平成21年1月14日