2.5
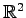 における直線の方程式
における直線の方程式
例 2.9 (
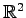 の直線の方程式の具体例)
点
の直線の方程式の具体例)
点 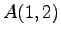 ,
, 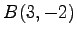 を通る直線の方程式を考える.
まず
を通る直線の方程式を考える.
まず
とおく.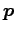 は方向ベクトルである.
直線の方程式のパラメータ表示は
は方向ベクトルである.
直線の方程式のパラメータ表示は
である.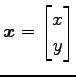 とおき
とおき 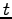 を消去すると,
直線の方程式の成分表示は
を消去すると,
直線の方程式の成分表示は
であり,変形して
である. 法線ベクトルは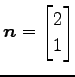 である.
さらに変形して
である.
さらに変形して
となる.傾きは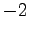 であり,
であり,
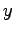 切片は
切片は  である.
さらに変形して
である.
さらに変形して
となる.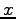 切片は
切片は  であり,
であり,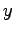 切片は
切片は  である.
である.
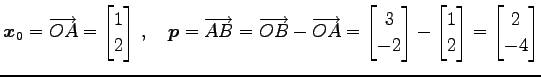 |
(23) |
とおく.
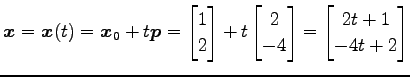 |
(24) |
である.
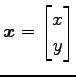 とおき
とおき 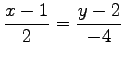 |
(25) |
であり,変形して
| (26) |
である. 法線ベクトルは
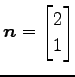 である.
さらに変形して
である.
さらに変形して
| (27) |
となる.傾きは
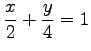 |
(28) |
となる.
例 2.10 (
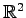 の直線の方程式の具体例)
点
の直線の方程式の具体例)
点 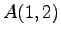 ,
, 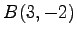 を通る直線の方程式を考える.
直線の方程式を
を通る直線の方程式を考える.
直線の方程式を
と仮定する. 点 ,
,  は直線上にあるので
は直線上にあるので
が成り立つ. この連立方程式を解くと
となる.直線の方程式を
と得る.
| (29) |
と仮定する. 点
| (30) |
が成り立つ. この連立方程式を解くと
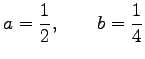 |
(31) |
となる.直線の方程式を
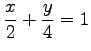 |
(32) |
と得る.
平成20年4月22日