1.3 複素数
定義 1.6 (複素数)
複素数(complex number)とは,
実数 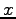 ,
, 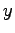 に対して
に対して  で定まる数である.
ただし
で定まる数である.
ただし 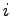 は
は 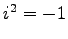 をみたし,
虚数単位(imaginary unit)と呼ぶ.
複素数
をみたし,
虚数単位(imaginary unit)と呼ぶ.
複素数  の
の 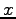 を実部(real part)といい
を実部(real part)といい
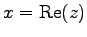 と表す.
と表す.
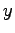 を虚部(imaginary part)といい
を虚部(imaginary part)といい
 と表す.
虚部が
と表す.
虚部が
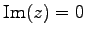 のとき
のとき
 は実数(real number)といい,
虚部が 0 でない複素数を虚数(imaginary number)といい,
実部が
は実数(real number)といい,
虚部が 0 でない複素数を虚数(imaginary number)といい,
実部が
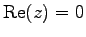 の虚数を
純虚数(pure imaginary number)という.
の虚数を
純虚数(pure imaginary number)という.
定義 1.7 (複素平面)
複素数全体の集合を
 と表す.
この集合を実部
と表す.
この集合を実部
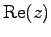 を横軸に
虚部
を横軸に
虚部
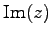 を縦軸にとることできる平面を
複素平面(complex plane)と呼ぶ.
このとき横軸を実軸(real axis)といい,
縦軸を虚軸(imaginary axis)という.
を縦軸にとることできる平面を
複素平面(complex plane)と呼ぶ.
このとき横軸を実軸(real axis)といい,
縦軸を虚軸(imaginary axis)という.
定義 1.8 (複素共役)
複素数  に対して複素数
に対して複素数
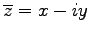 を
を
 の複素共役(complex conjugate)という.
の複素共役(complex conjugate)という.
定義 1.9 (複素数の絶対値と偏角)
複素数  に対して実数
に対して実数
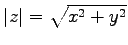 を
を
 の絶対値(absolute value)
または大きさ(modulus)という.
の絶対値(absolute value)
または大きさ(modulus)という.
 を
を  の
偏角(argument)という.
の
偏角(argument)という.
注意 1.10 (複素数の絶対値と偏角)
複素平面上で原点 0 とあるある複素数  との
距離は
との
距離は  の絶対値
の絶対値
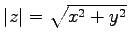 である.
また,実軸と 2 点 0,
である.
また,実軸と 2 点 0,  を通る直線とのなす角は
を通る直線とのなす角は
 の偏角
の偏角
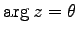 である.
ただし,
である.
ただし,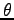 は
は
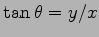 をみたせばよいので,
をみたせばよいので,
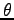 に
に 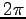 の整数倍を加えたものもまた偏角であるから,
の整数倍を加えたものもまた偏角であるから,
と任意性がある. 特に,偏角のなかで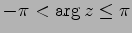 をみたすものを
偏角の主値とよび
をみたすものを
偏角の主値とよび
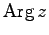 と書くことにする.
と書くことにする.
| (1) |
と任意性がある. 特に,偏角のなかで
定義 1.11 (極形式)
複素数  は
は
と表せる.これを複素数の極形式という.
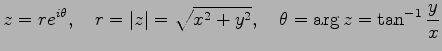 |
(2) |
と表せる.これを複素数の極形式という.
定義 1.12 (オイラーの公式)
| (3) |
注意 1.13 (複素数の演算)
複素数  ,
, 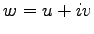 に対して
次の四則演算が成り立つ:
に対して
次の四則演算が成り立つ:
| (4) | ||
| (5) | ||
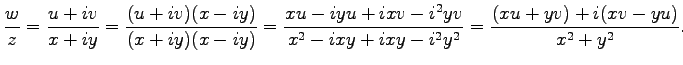 |
(6) |
定理 1.14 (複素数の性質)
次の性質が成り立つ:
(1)
![]() (2)
(2)
![]() .
(3)
.
(3)
![]() .
(4)
.
(4)
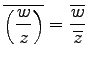 (5)
(5)
![]()
(6)
![]() (7)
(7)
 (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]()
(11)
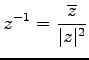 (12)
(12)
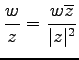 (13)
(13)
 (14)
(14)

(15)
![]()
![]()
![]() は実数.
(16)
は実数.
(16)
![]()
![]()
![]() は純虚数.
(17)
は純虚数.
(17)
![]()
(18)
 (19)
(19)
![]()
問 1.15 (複素数の性質)
これらの性質を示せ.
例 1.16 (極形式)
複素数 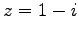 の大きさは
の大きさは
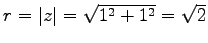 であり,
偏角は
であり,
偏角は
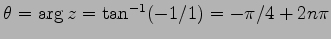 である.
である.
 の極形式は
の極形式は
となる.
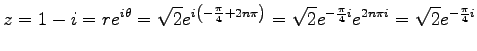 |
(7) |
となる.
例 1.17 (極形式)
複素数 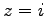 の大きさは
の大きさは
 であり,
偏角は
であり,
偏角は
 である.
である.
 の極形式は
の極形式は
となる.
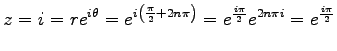 |
(8) |
となる.
例 1.18 (べき乗の根)
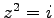 をみたす複素数
をみたす複素数  を求める.
極形式にして式変形すると
を求める.
極形式にして式変形すると
を得る.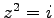 の両辺に根号をとると
の両辺に根号をとると
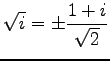 が成り立つ.
が成り立つ.
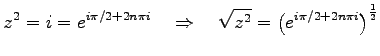 |
(9) | |
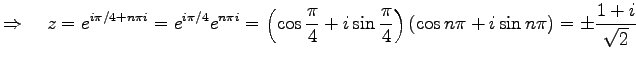 |
(10) |
を得る.
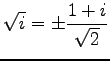 が成り立つ.
が成り立つ.
例 1.19 (多項式の根)
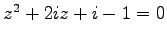 の根を求める.
実数と同じように解の公式を用いると
の根を求める.
実数と同じように解の公式を用いると
となる.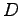 を極形式で表すと
を極形式で表すと
であるから,
となり,
を得る.
| (11) |
となる.
| (12) |
であるから,
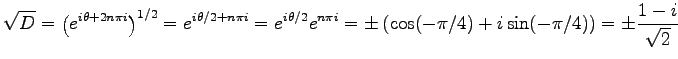 |
(13) |
となり,
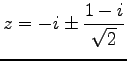 |
(14) |
を得る.
平成20年4月22日