2.4 演習問題 〜 関数,極限,連続
問 2.20 (2 変数関数)
関数
 に対して次の値を求めよ.
に対して次の値を求めよ.
(1) (2)
(2)  (3)
(3)  (4)
(4) 
(1)
問 2.21 (2 変数関数)
次の関数  のグラフ
のグラフ 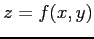 を描け.
(ヒント:平面
を描け.
(ヒント:平面
 ,
,
 による切口の図形を考える.)
による切口の図形を考える.)
(1)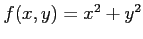 (2)
(2)

(1)
問 2.22 (2 変数関数)
次の関数  のグラフ
のグラフ 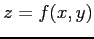 の
の  平面,
平面,
 平面による切口の図形を描け.
平面による切口の図形を描け.
(1)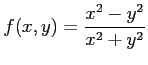 (2)
(2)

(1)
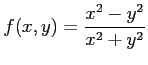 (2)
(2)

問 2.23 (極限)
次の極限を求めよ.
(1)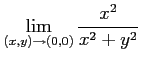 (2)
(2)
 (3)
(3)
 (4)
(4)
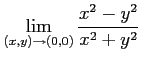
(5)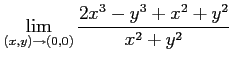 (6)
(6)
 (7)
(7)
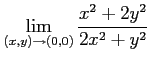
(8) (9)
(9)
 (10)
(10)
 (11)
(11)

(12) (13)
(13)
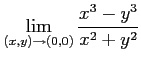 (14)
(14)

(1)
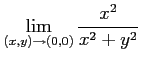 (2)
(2)
 (3)
(3)
 (4)
(4)
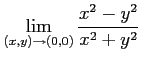
(5)
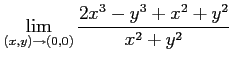 (6)
(6)
 (7)
(7)
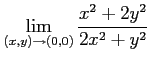
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)

(12)
 (13)
(13)
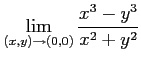 (14)
(14)

問 2.24 (連続)
次の関数  が原点で連続となるか議論せよ.
ただし
が原点で連続となるか議論せよ.
ただし 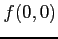 は適当に定義せよ.
は適当に定義せよ.
(1)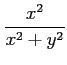 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6) 
(7) (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)

(13) (14)
(14)
 (15)
(15)

(1)
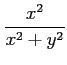 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6) (7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)

(13)
 (14)
(14)
 (15)
(15)
平成21年12月2日