2.5 多変数関数の微分
1 変数関数 ![]() において,
において,
![]() から
から
![]() への
への ![]() の増分は
の増分は
である. このとき,
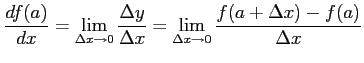 |
である. このとき
一方,2 変数関数 ![]() においては,
定義域
においては,
定義域 ![]() 内の点
内の点 ![]() から
点
から
点
![]() への
への ![]() の増分
の増分
を考える. このとき
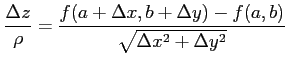 |
となる. ただし,
- (i).
- 全方向
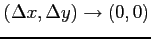 から近づけたとき,
傾き
から近づけたとき,
傾き
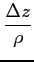 の極限が
存在すれば,
の極限が
存在すれば, は全微分可能であるという.
は全微分可能であるという.
- (ii).
 軸に沿って
軸に沿って
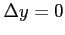 ,
,
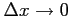 (
(
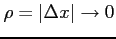 )と近づけたとき,
傾きの極限
)と近づけたとき,
傾きの極限
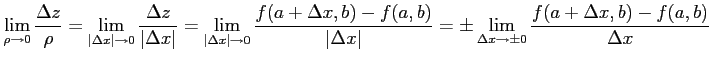
が存在すれば, は
は に関して偏微分可能であるという.
に関して偏微分可能であるという.
- (iii).
 軸に沿って
軸に沿って
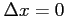 ,
,
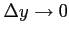 (
(
 )と近づけたとき,
傾きの極限
)と近づけたとき,
傾きの極限
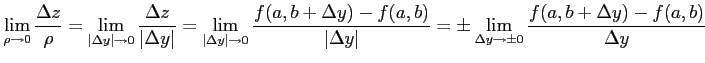
が存在すれば, は
は に関して偏微分可能であるという.
に関して偏微分可能であるという.
平成21年12月2日