2.7 多変数関数の偏微分
定義 2.33 (多変換数の導関数)
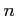 変数関数
変数関数
 の
偏導関数は
の
偏導関数は
と定義する. ただし,
とおく.
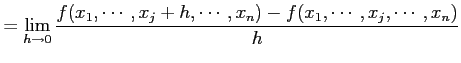 |
||
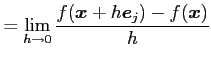 |
と定義する. ただし,
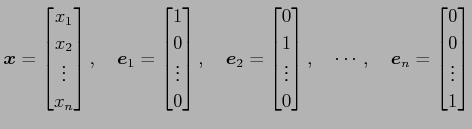 |
とおく.
例 2.34 (多変換数の導関数)
関数
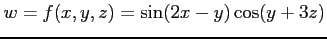 の
偏導関数は,
の
偏導関数は,
となる.
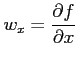 |
||
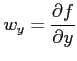 |
||
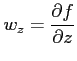 |
となる.
例 2.35 (多変換数の導関数)
関数
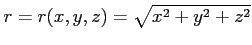 の
偏導関数は,
の
偏導関数は,
となる.
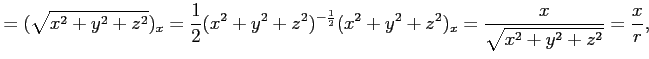 |
||
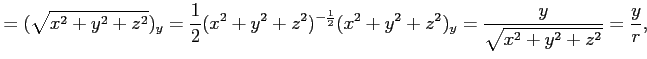 |
||
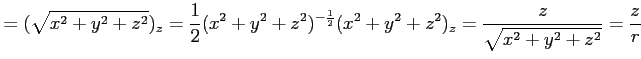 |
となる.
平成21年12月2日