2.39 接線
注意 2.171 (曲線の法線ベクトル)
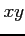 平面内の曲線
平面内の曲線  上の点を
パラメータ表示し,
上の点を
パラメータ表示し,
 とおく.
このとき,曲線上の 2 点
とおく.
このとき,曲線上の 2 点
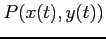 ,
,
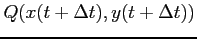 は
は
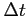 が十分小さいときテイラー展開して
が十分小さいときテイラー展開して
と表される.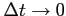 のとき,
ベクトル
のとき,
ベクトル
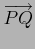 の向きと
接線の方向ベクトル
の向きと
接線の方向ベクトル 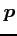 の向きは等しくなる.
よって,
接線の方向ベクトルは
の向きは等しくなる.
よって,
接線の方向ベクトルは
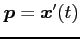 である.
一方,
である.
一方,
 の両辺を
の両辺を 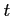 で微分すると
で微分すると
となる.ベクトルで表すと
となる. は
は
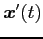 と直交する.
よって,接線の法線ベクトルは
と直交する.
よって,接線の法線ベクトルは
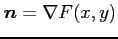 である.
である.
と表される.
となる.ベクトルで表すと
となる.
定理 2.172 (接線)
曲線  の点
の点 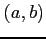 における
接線の方程式は
における
接線の方程式は
で与えられる.ベクトルで表記すると
となる.
である.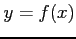 の
の 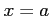 における接線の方程式は
における接線の方程式は
と表される.ただし,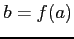 とおく.
とおく.
で与えられる.ベクトルで表記すると
となる.
(証明)
接線は点 ![]() を通り,
法線ベクトルが
を通り,
法線ベクトルが
![]() の直線であるので,
の直線であるので,
![]() を得る.
または,次のようにも示される.
条件
を得る.
または,次のようにも示される.
条件 ![]() により定義される陰関数
により定義される陰関数 ![]() を考える.
このとき
を考える.
このとき ![]() の導関数は
の導関数は
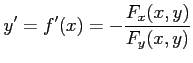 |
である.
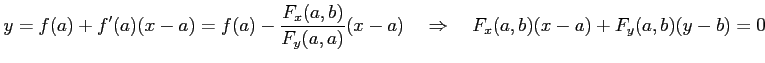 |
と表される.ただし,
例 2.173 (接線の方程式)
円
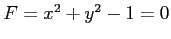 の点
の点 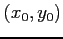 における
接線の方程式を求める.
接線の法線ベクトルは
における
接線の方程式を求める.
接線の法線ベクトルは
を用いて であり,
点
であり,
点 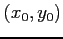 を通る直線であるから,
を通る直線であるから,
を得る.
を用いて
を得る.
例 2.174 (接線の方程式)
曲線
 の点
の点 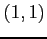 における
接線の方程式を求める.
まず,曲線の方程式を書き直して
における
接線の方程式を求める.
まず,曲線の方程式を書き直して
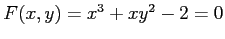 とおく.
このとき,
とおく.
このとき,
であり,点 を代入して
を代入して
となる. 接線の方程式は
であり, 書き直すと
を得る. 法線ベクトルが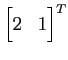 の直線である.
の直線である.
であり,点
となる. 接線の方程式は
であり, 書き直すと
を得る. 法線ベクトルが
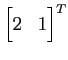 の直線である.
の直線である.
例 2.175 (接線の方程式)
曲線
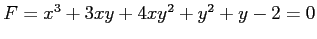 の点
の点 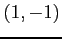 における
接線の方程式を求める.
における
接線の方程式を求める.
より,接線は
と得られる. 法線ベクトルが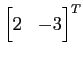 の直線である.
方程式を書き直して
の直線である.
方程式を書き直して
とする. 接線の傾きは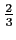 で
で  切片は
切片は
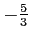 である.
である.
と書き直す. 接線の 切片は
切片は
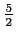 で
で  切片は
切片は
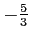 である.
である.
より,接線は
と得られる. 法線ベクトルが
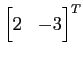 の直線である.
方程式を書き直して
の直線である.
方程式を書き直して
 |
とする. 接線の傾きは
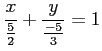 |
と書き直す. 接線の
平成21年12月2日