2.40 2 変数の陰関数
定義 2.176 (陰関数)
変数  ,
,  ,
,  が条件
が条件
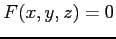 をみたすとき,
をみたすとき,
 は
は  ,
,  の関数
の関数 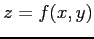 であるとみなせる.
すなわち,
であるとみなせる.
すなわち,
により定義される関数 を,
を,
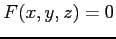 で定義される陰関数(implicit function)という.
で定義される陰関数(implicit function)という.
により定義される関数
例 2.177 (陰関数)
条件
により定まる陰関数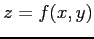 の偏導関数を求める.
の偏導関数を求める.
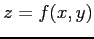 を代入すると
を代入すると
となる.両辺を で偏微分すると
で偏微分すると
となので,
を得る.同様にして で偏微分すると
で偏微分すると
となるので,
を得る.
により定まる陰関数
となる.両辺を
となので,
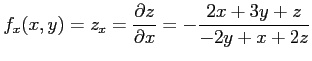 |
を得る.同様にして
となるので,
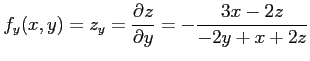 |
を得る.
定理 2.178 (陰関数の微分)
条件
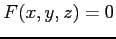 で定義される陰関数
で定義される陰関数 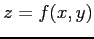 の偏導関数は,
の偏導関数は,
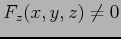 のとき
のとき
で与えられる.
となるので,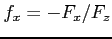 を得る.
同様にして
を得る.
同様にして  で偏微分すると
で偏微分すると
となるので,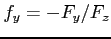 を得る.
を得る.
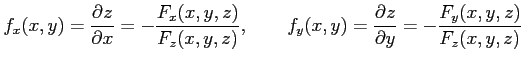 |
で与えられる.
(証明)
条件
![]() に
に ![]() を代入して,
両辺を
を代入して,
両辺を ![]() で偏微分すると
で偏微分すると
| 0 | 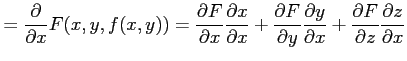 |
|
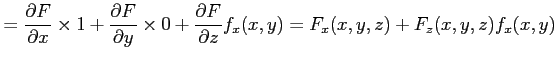 |
となるので,
| 0 | 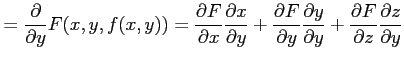 |
|
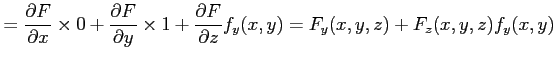 |
となるので,
例 2.179 (陰関数)
条件
により定まる陰関数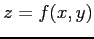 の偏導関数を求める.
まず,
の偏導関数を求める.
まず,
より,偏導関数は
と得られる.
により定まる陰関数
より,偏導関数は
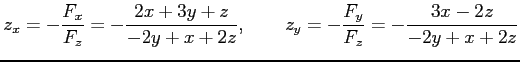 |
と得られる.
例 2.180 (陰関数)
条件
により定まる陰関数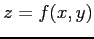 の 2 階偏導関数
の 2 階偏導関数
 ,
, 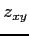 ,
, 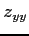 を求める.
条件
を求める.
条件  の両辺を
の両辺を  で偏微分すると
で偏微分すると
である.さらに で偏微分すると
で偏微分すると
となるから,
を得る. (☆)の両辺を で偏微分すると
で偏微分すると
となるから,
を得る. 条件 の両辺を
の両辺を  で偏微分すると
で偏微分すると
である.さらに で偏微分すると
で偏微分すると
となるから,
を得る.
により定まる陰関数
である.さらに
| 0 | ||
となるから,
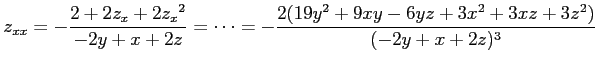 |
を得る. (☆)の両辺を
| 0 | ||
となるから,
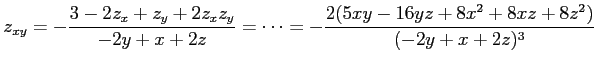 |
を得る. 条件
である.さらに
| 0 | ||
となるから,
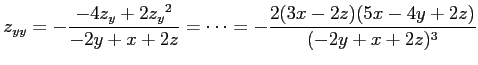 |
を得る.
平成21年12月2日