2.50 演習問題 〜 極値
問 2.231 (極値)
次の関数  の極値をすべて求めよ.
の極値をすべて求めよ.
(1)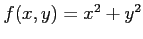 (2)
(2)
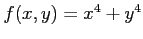 (3)
(3)
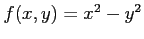 (4)
(4)
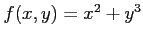
(5)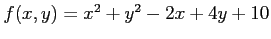 (6)
(6)
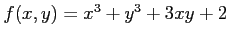
(7)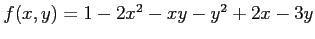 (8)
(8)
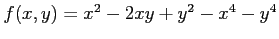
(9)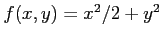 (10)
(10)
 (11)
(11)
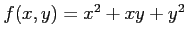
(12)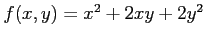 (13)
(13)
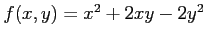 (14)
(14)
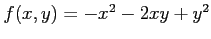
(15)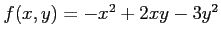 (16)
(16)
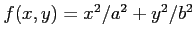
(17)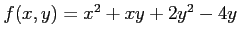 (18)
(18)
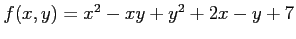
(19)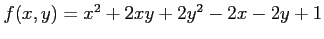 (20)
(20)
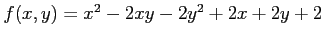
(21)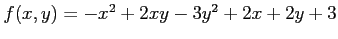 (22)
(22)
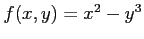 (23)
(23)
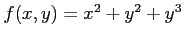
(24) (25)
(25)
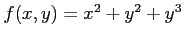 (26)
(26)
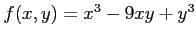
(27)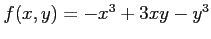 (28)
(28)

(29) (30)
(30)
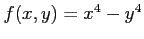
(31)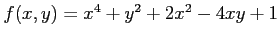 (32)
(32)

(33)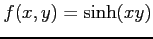 (34)
(34)
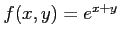 (35)
(35)
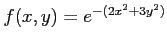
(1)
(5)
(7)
(9)
(12)
(15)
(17)
(19)
(21)
(24)
(27)
(29)
(31)
(33)
問 2.232 (陰関数の極値)
次の条件で定められる陰関数 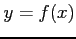 の極値をすべて求めよ.
の極値をすべて求めよ.
(1)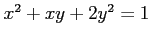 (2)
(2)
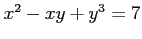
(1)
問 2.233 (条件付き極値)
次の条件 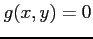 のもとでの関数
のもとでの関数  の極値をすべて調べよ.
の極値をすべて調べよ.
(1)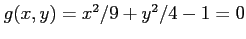 ,
,
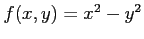
(2)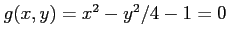 ,
,
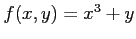
(3)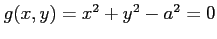 ,
,
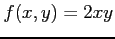
(4)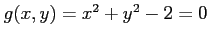 ,
,
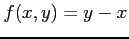
(5) ,
, 
(6)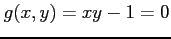 ,
,
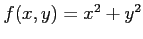
(7)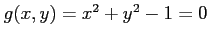 ,
,
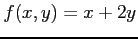
(8) ,
, 
(9)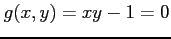 ,
,
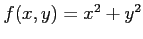
(10)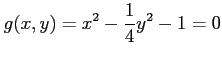 ,
,
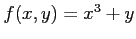
(11)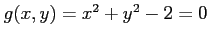 ,
,
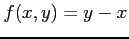
(12)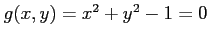 ,
,
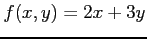
(13)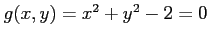 ,
, 
(14)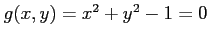 ,
,
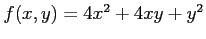
(15)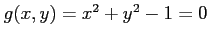 ,
,
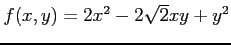
(16)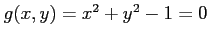 ,
,
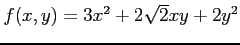
(17)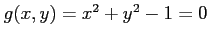 ,
,
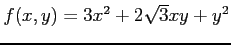
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
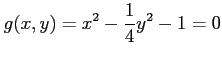 ,
,
(11)
(12)
(13)
(14)
(15)
(16)
(17)
問 2.234 (領域内の最大値,最小値)
次の関数  の領域
の領域
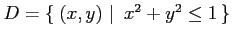 における
最大値,最小値を求めよ.
における
最大値,最小値を求めよ.
(1)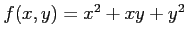 (2)
(2)
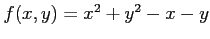
(1)
平成21年12月2日