3.2 累次積分
定義 3.12 (簡単な領域)
領域 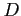 が
が
と表されるとき,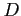 を
を に関して簡単な領域という.
に関して簡単な領域という.
と表されるとき,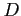 を
を に関して簡単な領域という.
に関して簡単な領域という.
と表されるとき,
と表されるとき,
定理 3.13 (累次積分)
領域 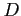 が
が  に関して単純なとき,
多重積分は定積分
に関して単純なとき,
多重積分は定積分
により与えられる. 領域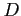 が
が  に関して単純なとき,
多重積分は定積分
に関して単純なとき,
多重積分は定積分
により与えられる. これらの積分を累次積分という.
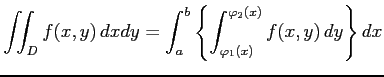 |
により与えられる. 領域
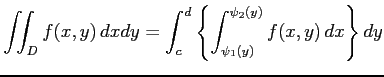 |
により与えられる. これらの積分を累次積分という.
注意 3.14 (累次積分)
累次積分は省略して次のように表記する:
 |
||
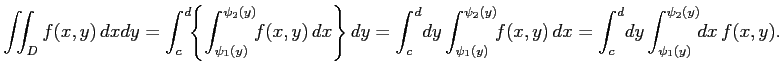 |
平成21年12月2日