3.4 3 重積分の計算
例 3.26 (累次積分)
3 重積分
を求める. 領域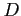 は 平面
は 平面  ,
, 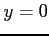 ,
, 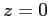 ,
, 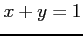 ,
, 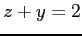 で囲まれて
できる領域である.
で囲まれて
できる領域である.
![\includegraphics[width=0.5\textwidth]{sekibun3-D1.eps}](img2046.png) 領域
領域 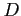 は
は  は
は  に関して単純であり,
に関して単純であり,
 は
は  ,
,  に関して単純な領域であるから,
累次積分を用いて計算して,
に関して単純な領域であるから,
累次積分を用いて計算して,
と得られる.
 |
を求める. 領域
![\includegraphics[width=0.5\textwidth]{sekibun3-D1.eps}](img2046.png)
![$\displaystyle =\int_{0}^{1}dx\int_{0}^{1-x}dy\int_{0}^{2-y}dz\,xyz= \int_{0}^{1...
...2}\,\right]_{z=0}^{z=2-y}= \int_{0}^{1}dx\int_{0}^{1-x}dy\,\frac{1}{2}xy(2-y)^2$](img2047.png) |
||
![$\displaystyle = \int_{0}^{1}dx\int_{0}^{1-x}dy\, \frac{1}{2}x(y^3-4y^2+4y)= \in...
...eft(\frac{y^4}{4}- \frac{4y^3}{3}+\frac{4y^2}{2}\right)}\,\right]_{y=0}^{y=1-x}$](img2048.png) |
||
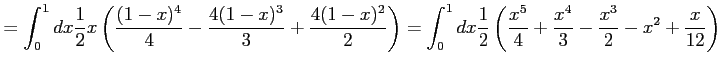 |
||
![$\displaystyle =\frac{1}{2} \left[\vrule height1.5em width0em depth0.1em\,{ \fra...
...rac{x^4}{8}-\frac{x^3}{3}+\frac{x^2}{24} }\,\right]_{x=0}^{x=1}= \frac{13}{240}$](img2050.png) |
と得られる.
問 3.27 (領域の面積)
領域 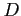 の体積
の体積
 を求めよ.
を求めよ.
例 3.28 (累次積分)
3 重積分
を求める. 領域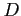 は 平面
は 平面  ,
, 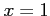 ,
,
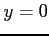 ,
, 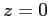 ,
, 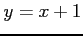 ,
, 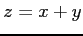 で囲まれてできる領域である.
で囲まれてできる領域である.
![\includegraphics[width=0.5\textwidth]{area3d_2.eps}](img2054.png) また,領域
また,領域 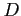 は
は  は
は  に関して単純であり,
に関して単純であり,
 は
は  ,
,  に関して単純な領域であるから,
累次積分を用いて計算して,
に関して単純な領域であるから,
累次積分を用いて計算して,
と得られる.
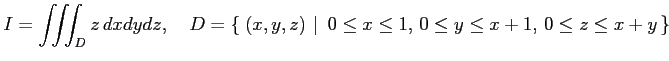 |
を求める. 領域
![\includegraphics[width=0.5\textwidth]{area3d_2.eps}](img2054.png)
![$\displaystyle = \int_{0}^{1}dx\int_{0}^{x+1}dy\int_{0}^{x+y}z\,dz= \int_{0}^{1}...
...^2}{2}}\,\right]_{z=0}^{z=x+y}= \int_{0}^{1}dx\int_{0}^{x+1}dy\frac{(x+y)^2}{2}$](img2055.png) |
||
![$\displaystyle = \int_{0}^{1}dx\left[\vrule height1.5em width0em depth0.1em\,{\f...
...h0.1em\,{\frac{(2x+1)^4}{48}-\frac{x^4}{24}}\,\right]_{x=0}^{x=1}= \frac{13}{8}$](img2056.png) |
と得られる.
問 3.29 (領域の面積)
領域 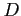 を図示し,
領域
を図示し,
領域 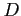 の体積
の体積
 を求めよ.
を求めよ.
例 3.30 (累次積分)
3 重積分
を求める. 領域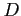 は原点を中心とする半径
は原点を中心とする半径 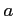 の球の内部で
の球の内部で
 ,
,  ,
,  が正の領域である.
領域
が正の領域である.
領域 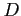 は
は
と書き直すと, 多重積分は累次積分を用いて計算できて,
となる. ここで, の定積分を
の定積分を
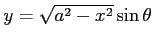 と置換積分すると,
と置換積分すると,
 の積分区間は
の積分区間は ![$ [0,\pi/2]$](img2062.png) であり,
であり,
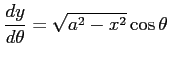 を用いると,
を用いると,
と求まる.
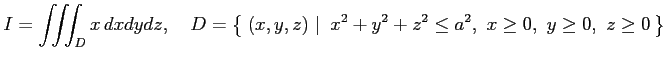 |
を求める. 領域
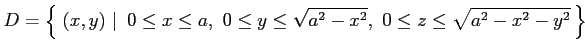 |
と書き直すと, 多重積分は累次積分を用いて計算できて,
![$\displaystyle = \int_{0}^{a}x\,dx \int_{0}^{\sqrt{a^2-x^2}}dy \int_0^{\sqrt{a^2...
...rule height1.5em width0em depth0.1em\,{z}\,\right]_{z=0}^{z=\sqrt{a^2-x^2-y^2}}$](img2059.png) |
||
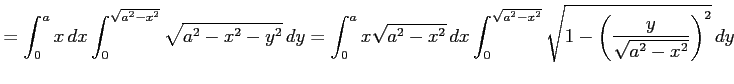 |
となる. ここで,
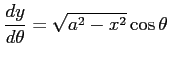 を用いると,
を用いると,
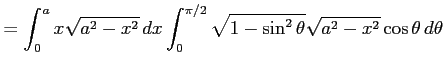 |
||
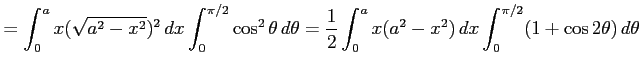 |
||
![$\displaystyle = \frac{1}{2} \int_{0}^{a}(a^2x-x^3)\,dx \left[\vrule height1.5em...
...epth0.1em\,{\frac{a^2x^2}{2}-\frac{x^4}{4}}\,\right]_{0}^{a}= \frac{\pi}{16}a^4$](img2066.png) |
と求まる.
平成21年12月2日