3.18 線積分
定義 3.85 (線積分)
関数
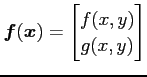 に対する有向曲線
に対する有向曲線
に関する線積分(line integral)を
と定義する. 曲線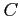 を積分路(integral path)という.
を積分路(integral path)という.
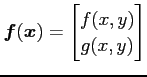 に対する有向曲線
に対する有向曲線
に関する線積分(line integral)を
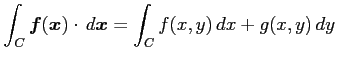 |
||
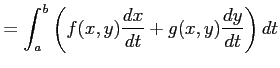 |
||
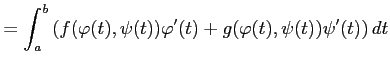 |
と定義する. 曲線
注意 3.86 (線積分)
定義より
 のとき
のとき
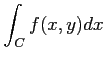 と表記し,
と表記し,
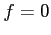 のとき
のとき
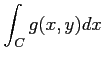 と表記する.
それぞれは,
と表記する.
それぞれは,
となるので,
と表記される.
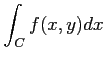 と表記し,
と表記し,
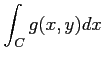 と表記する.
それぞれは,
と表記する.
それぞれは,
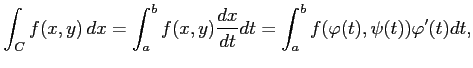 |
||
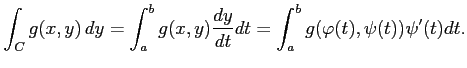 |
となるので,
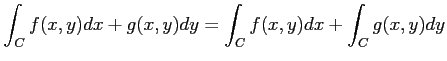 |
と表記される.
注意 3.87 (線積分)
線積分は力学の仕事(work)である.
力  を加えて距離
を加えて距離
 移動したときの
仕事は
移動したときの
仕事は
 である.
経路
である.
経路 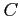 に沿って移動させたときの仕事の総和は
に沿って移動させたときの仕事の総和は
となる.
 |
となる.
定理 3.88 (線積分)
次の関係が成り立つ:
(i)
 (ii)
(ii)
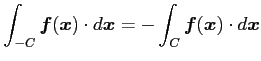
例 3.89 (線積分)
線積分
を求める. ,
,
 を用いて,線積分は
を用いて,線積分は
と求まる.
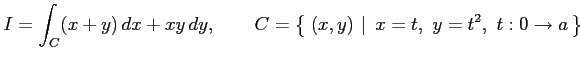 |
を求める.
 ,
,
 を用いて,線積分は
を用いて,線積分は
![$\displaystyle = \int_{0}^{a}\left((t+t^2)\frac{dx}{dt}+t\cdot t^2\frac{dy}{dt}\...
...3}+\frac{2t^5}{5}}\,\right]_{0}^{a}= \frac{a^2}{2}+\frac{a^3}{3}+\frac{2a^5}{5}$](img2471.png) |
と求まる.
平成21年12月2日