3.19 経路の異なる積分路における線積分
例 3.90 (線積分)
点 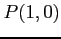 から点
から点  への経路を
への経路を
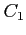 と
と 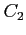 の 2 通りを考える.
の 2 通りを考える.
とする. このとき線積分は
となる.
とおく.線積分は
となる.
(i)
積分路 ![]() は
は ![]() から
から ![]() へ直線的に進むとして,
へ直線的に進むとして,
とする. このとき線積分は
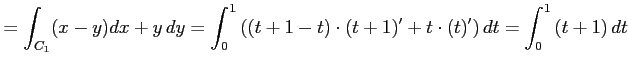 |
||
![$\displaystyle = \left[\vrule height1.5em width0em depth0.1em\,{\frac{t^2}{2}+t}\,\right]_{0}^{1}=\frac{3}{2}$](img2479.png) |
となる.
(ii)
積分路 ![]() は
は ![]() から点
から点 ![]() を経由し
を経由し ![]() へ直線的に進むとして,
へ直線的に進むとして,
とおく.線積分は
 |
||
 |
||
![$\displaystyle = \int_{0}^{1}\left(t+1\right)dt+ \int_{0}^{1}t\,dt= \int_{0}^{1}...
...ht)dt= \left[\vrule height1.5em width0em depth0.1em\,{t^2+t}\,\right]_{0}^{1}=2$](img2486.png) |
となる.
注意 3.91 (線積分)
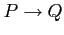 への積分路が異なれば積分値も異なる.
への積分路が異なれば積分値も異なる.
定義 3.92 (線積分)
点 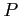 から点
から点 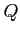 への経路によらず線積分が同じとき,
その線積分を
への経路によらず線積分が同じとき,
その線積分を
と書く.
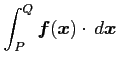 |
と書く.
平成21年12月2日